Higher throughput of smaller machinery

The bottommost microscopically thin layer has the exact same throughput as the topmost macroscopic one. Thus filling the whole volume with nanomachinery would lead to exorbitant throughput and exorbitant waste heat. This is neither necessary nor desirable. All layers are operating at the exact same speed (not same frequency). Chosen here is a branching factor of four for illustrative purposes only. – While this is related to convergent assembly in the form of assembly layers. This specific topology and geometry does not match any concretely proposed designs. Actually (via exploratory engineering) proposed designs have significant deviations from this.

Video: "The Surprising Productivity of Nano-Machinery"
Short preview version: "Convergent Assembly and its effect on friction in Cog-and-Gear-style Nanomachinery"
When production machines are made smaller
(but are still operated at the same unchanged speed)
then they can produce more product per time.
- Halve sized machinery has double the throughput per volume of machinery.
- Ten times smaller machinery has ten times the throughput per volume of machinery.
- A million times smaller machinery has a million times the throughput per volume of machinery.
At that point other effects become mixed in though.
In short: It is a linear scaling law.
For the math behind why this scaling law applies see:
Math of convergent assembly
Contents
[hide]- 1 Limits
- 2 Some basic intuition
- 3 Basic math
- 4 From the perspective of diving down into a prospective nanofactory
- 5 Getting silly – questionable and unnecessary productivity levels
- 6 Relation to Convergent assembly
- 7 Lessening the macroscale throughput bottleneck
- 8 Alternate names for this scaling law as a concept
- 9 Related
- 10 External links
Limits
Important fact:
This scaling law does not take under consideration
- the necessary ingress of resource supply and
- the necessary removal of the product
And this is ok as long as these contribute only a tiny fraction of the total friction losses
But once transport motions become dominant in contribution of friction losses the scaling law breaks down.
The bigger the branching factor B, the more there can be gained form this scaling law.
Concretely: The optimal sub-layer number where total frictionloss is mimimal is B³.
Beyond that friction goes up again (eventually linearly). The scaling law breaks down.
This happens to also be the point where assembly friction losses and transport friction losses are equal.
For derivation of these results see page: Optimal sublayernumber for minimal friction
(wiki-TODO: Make a infographic here in analogy to the one the page Level throughput balancing)
Some basic intuition
How the heck can throughput rise when the very first assumption was
that speed of robotic manipulation will be kept constants over all size scales?!
The answer:
- In place assembly is assumed here.
- Removal of the assembled product from the manufacturing structure (the scaffold) is not included.
- This looks at assembly motions only.
The necessary transport motions that emerge when nanomachinery is stacked beyond the macroscale slowness bottleneck are for now ignored.
See: Multilayer assembly layers for how these motions relate to each other.
No, part removal for densely packed nanomachinery is not a problem
in the case of basic gem-gum factories where:
- (1) there is no densely packed nanomachinery
instead a stack of one monolayer of each assembly level is the baseline design which:
– makes throughput constant over all size scales (see math section below) and
– makes removal of the assembled product from the manufacturing structure correspond to pusing products up in the next assembly level (where streaming further up continues) - (2) the bottom assembly level is a thicker stack (a multilayer slab) that has much lower assembly speeds than transport speeds.
Warning! you are moving into more speculative areas.
Higher degrees of filling space with nanomachinery than just thin monolayers may not be completely impossible.
It would certainly be way beyond everyday practical.
Transport speeds for product removal would "just" need to be faster than what is robotically possible.
Imaginable would e.g. be a ultra high throughput microcomponent recomposer unit that is a block full of nanomachinery that has lots of straight coaxial high speed product shootout channels with stratified shear bearings. It would also need significant active cooling.
Related: Producer product pushapart
Visualizing the assembly speed difference by animation
Imagine unassembled block-fragments (color coded red) on the bottom of an robotic assembly cell
being assembled by the robotic mechanism inside of the cell
to one product block (color coded green) at the top of the cell.
Taking just one big macroscopic cell this process takes a while since all the parts need to travel the macroscopic distance from the bottom of the big assembly cell to the the top to turn from red to green.
When instead taking many small robotic cells (that have with their robotics inside moving with the same speed) the distance from red to green is much shorter and thus everything turns from red (unassembled) to green (assembled) much much faster.
Advanced Q&A:
Why is the transition from red unassembled to green assembled
in a 2D monolayer of robotic assembly cells faster than in one big cell of same 2D cross section?
Isn't it supposed to finish in the same time if it's just a single monolayer?
You're looking a a cross section!
The red to green transition in a single monolayer is indeed way faster.
But that single monolayer needs to repeat that transition many times over in order to
make up for all the other the other layers that would be needed to completely fill up the volume of the big cell.
In the simple model this exactly cancels out.
(wiki-TODO: make (that is program) that animation – via OpenSCAD or Blender)
Basic math
(1) Take a cube with some robotic cog and gear assembly machinery of unspecified nature inside.
(2) Replace the contents of the cube with several scaled down copies of the original cube. A whole numbered cuberoot is advantageous.
(3) How does the throughput change in terms of how much volume can be assembled per unit of time?
Used constants:
- n = 1 ... one robotic unit in one robotic cell – this is just here to not mix it up with other dimensionless numbers
- s ... sidelength of the product blocks that the robotic unit assembles
s^3 ... volume
rho*s^3 ... mass - f ... frequency of operation that is how often per unit of time a block assembly gets finished
- v ... constant speed for robotics on all size scales (crude approximation)
- Q ... throughput in terms of assembled volume per time
Full volume filled with robotics of original size
Throughput of one robotic cell:
Q = (n * s^3 * f)
Full volume filled with robotics of halve size
Throughput of eight robotic cells that
- are two times smaller each
- fill the same volume
- operate at the same speed:
(same speed means same magnitude of velocity not same frequency)
Q° = (n' * s'^3 * f') where n' = 2^3 n and s' = s/2 and f' = 2f
Q° = (2^3 n) * (s/2)^3 * (2f)
Q° = 2 * (n * s^3 * f)
Q° = 2Q
The ring ° could be interpreted as:
The whole volume gets filled with smaller machinery.
Full volume filled with robotics of 1/10th size
Throughput of a thousand robotic cells that
- are ten times smaller each
- fill the same volume
- operate at the same speed:
Q°° = (10^3 n) * (s/10)^3 * (10f)
Q°° = 10 * (n * s^3 * f)
Q°° = 10Q
Generalization to arbitrary size steps was avoided here because
it reduces comprehensibility.
One monolayer filled with robotics of 1/32th size
An actual practical nanofactory would (in first approximation) fill just one single monolayer.
- That means the smaller machinery matches the bigger machinery in throughput (Q' = Q).
- That is indeed done in order to match the throughput of the differently sized machiners such that they can be matchingly stacked.
Throughput of a hundred robotic cells that:
- are ten times smaller each
- fill 1/10th of same volume
- operate at the same speed:
Q' = (32^2 n) * (s/32)^3 * (32f)
Q' = (n * s^3 * f)
Q' = Q
The dash ' could be interpreted as:
Only a 2D monolayer gets filled with smaller robotic cell machinery.
The size step of 32 here makes for somewhat more realistic numbers.
- This way two convergent assembly steps make a nice size step of a 1000.
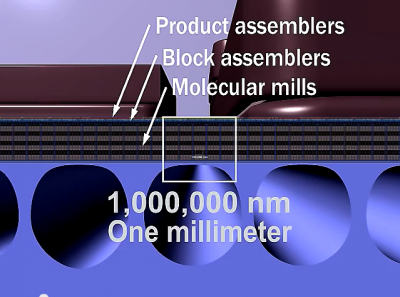
- This way four convergent assembly steps make a factor of a million which bridges big nano (~32nm) to small macro (~32mm)
Supplemental: Scaling of frequency
The unexplained scaling of frequency is rather intuitive.
Going back and forth halve the distance with the speed you get double the frequency.
If you really want it formally then here you go:
f = v/(constant*s) ~ v/s
f' ~ v/s' ~ v/(s/2) ~ 2f
From the perspective of diving down into a prospective nanofactory
Simplified nanofactory model
Let's for simplicity assume that the convergent assembly architecture in an advanced gem-gum factory is organized
- in simple coplanarly stacked assembly layers.
- that are each only one assembly cell in height, monolayers so to say
- that all operate at the same speed
Here ignored model deviations
There are good reasons to significantly deviate from that simple-most model.
Especially for the lowest assembly levels. E.g.
- high energy turnover in mechanosynthesis and
- fast recycling of pre-produced microcomponents and
- high bearing area
But the focus here is on conveying a baseline understanding.
And for assembly layers above the lowermost one(s) the simple-model above might hold quite well.
Same throughput of successively thinner layers
When going down the convergent assembly level layer stack …
- from a higher layer with bigger robotic assembly cells down
- to a the next lower layer with (much) smaller robotic assembly cells
… then one finds that the throughput capacity of both of these layers needs to be equal.
- If maximal throughput capacity would rise when going down the stack then the upper layers would form a bottleneck.
- If maximal throughput capacity would fall when going down the stack then the upper layers would be underutilized.
See main article: Level throughput balancing
The important thing to recognize here is that
while all the mono-layers have the same maximal product throughput
the thickness of these mono-layers becomes thinner and thinner.
More generally the volume of these layers becomes smaller and smaller.
So the throughput per volume shoots through the roof.
That is a very pleasant surprise!
In a first approximation halving the size of manufacturing robotics doubles throughput capacity per volume.
That means going down from one meter to one micrometer (a factor of a million)
the throughput capacity per volume equally explodes a whopping millionfold.
This is because it's a is a linear scaling law.
As mentioned this can't be extended arbitrarily though.
Below the micrometer level several effects (mentioned above) make
full exploitation of that rise in productivity per volume impossible.
Getting silly – questionable and unnecessary productivity levels
Now what if one would take a super thin microscale (possibly non-flat) assembly mono-"layer" that one finds pretty far down the convergent assembly stack and fills a whole macroscopic volume with many copies of it?
The answer is (in case of general purpose gem-gum factories) that the product couldn't be removed/expulsed fast enough. One hits fundamental acceleration limits (even for the strongest available diamondoid metamaterials) and long before that severe problems with mechanical resonances are likely to occur.
Note that the old and obsolete idea of packing a volume full with diamondoid molecular assemblers wouldn't tap into that potential because these devices are below the microscale level in the nanoscale where the useful behavior of physics of raising throughput density with falling size of assembly machinery is hampered by other effects.
More on silly levels of throughput here:
Relation to Convergent assembly
Instead of filling the whole volume with nanomachinery which would provide waay more productivity than in allmost all conceivable circumstances needed nanofactories would use only monolayers (or thin stacks).
In a first approximation successively stacked monolayers of consecutive assembly levels (and thus vastly different sizes) match in their maximal throughput. See: Level throughput balancing
And that despite the thickness of the layers with smaller machinery being insignificant compared to the thickness of the layers above. With the major exception of the bottommost assembly layers where things diverge notably from the first approximation.
Antagonistic effects/laws – sub microscale
The problem that emerges at the nanoscale is twofold.
- falling size => rising bearing area per volume => rising friction => to compensate: lower operation speed (and frequency) – summary: lower assembly event density in time
- falling size => rising machinery size to part size (atoms in the extreme case) – summary: lower assembly site density in space
Due to the nature of superlubricating friction:
- it scales with the square of speed (halving speed quaters friction losses)
- it scales linear with surface area (doubling area doubles friction)
It makes sense to slow down a bit and compensate by stacking layers for level throughput balancing. A combination of halving speed and doubling the number of stacked equal mono-"layers" halves friction while keeping throughput constant.
Lessening the macroscale throughput bottleneck
There are also effects/laws (located in the macroscale) that can help increase throughput density above the first approximation. Details on that can be found (for now) on the "Level throughput balancing" page.
Alternate names for this scaling law as a concept
- Higher throughput-density of smaller machinery (more precise & more cumbersome naming)
- Higher productivity of smaller machinery (well not all stuff made may be a desirable products, pessimistic view)
- Productivity explosion (too over-hyping & unspecific)
The thing is higher throughput does not necessarily means higher productivity in the sense of generation of useful products.
Thus the rename to the current page name "Higher throughput of smaller machinery".
Related
- Math of convergent assembly
- High performance of gem-gum technology
- Harvesting the benefits of the scaling law: Hyper high throughput microcomponent recomposition
- Deliberate slowdown at the lowest assembly level & Increasing bearing area to decrease friction
- Friction
- Scaling law -- Scaling law#Speedup
- Convergent assembly
- Level throughput balancing
- Macroscale slowness bottleneck
- Atom placement frequency
- Low speed efficiency limit
- Pages with math
- Optimal sublayernumber for minimal friction
- Another very important as of 2022 barely known scaling law:
Same relative deflections across scales - How macroscale style machinery at the nanoscale outperforms its native scale
- Slightly violated baseline scaling law: Same absolute speeds for smaller machinery
Another massively overpowered performance parameter is:
- Higher power density of smaller machinery.
That is less of a scaling law and more of a property of gem-gum systems though (TODO: to check).
