Optimal sublayernumber for minimal friction
This page is about aspects on how to design gemstone metamaterial on-chip factories
in order to minimize losses from friction.
Specifically looked at here are friction losses in a single assembly level/assembly layer of such a device.
Sought is finding the optimal number sub-layers.
Contents
- 1 Explanation of goals here
- 2 Math
- 3 Analysis of result
- 4 Legend/Key for the variables
- 5 Concerns about input side transport bearing area (and friction)
- 6 Furthermore
- 7 Math – relating to the compenslow design parameter
- 8 Are there alternate limits?
- 9 Very important note
- 10 Related
- 11 External links
Explanation of goals here
- There is an optimal number of layers for which total friction for a given throughput T and branching factor B is minimal
- There is an number of layers for which friction from transport motion crosses and then exceeds the friction loses from assembly motions.
The aim here to derive formulas for these layer numbers respectively
- the optimal layernumber n_opt
- the equal-friction layernumber n_eq
From a different perspective:
With (linearly) rising number of sub-layers:
- friction from assembly motions falls (linearly ~ 1/n).
- friction from transport motions rises (linearly ~ n).
Thus friction from transport motions poses a limit to exploiting:
(wiki-TODO: Come up with some example numbers for a quantitative plot eventually.)
Brief explanation of the premise
Assuming constant throughput:
Why does the friction drop with increasing layer numbers for low layer numbers?
Because while the bearing area grows the operation speeds fall.
And while the area makes the friction grow linearly the speed makes the friction fall quadratically.
See: Higher throughput of smaller machinery & Math of convergent assembly
BUT the transport speed does NOT fall when adding more layers.
Transport speed stays constant when adding more layers.
Transport-friction grows linearly with layer numbers but more importantly
Transport friction can only be ignored so long as assembly motions are much faster than transport motions.
Math
Let's consider:
- one single vertical stack of assembly cells n layers high.
- a parallel vertical stack of transport cells crossing the full height of these layers.
Speed relation from equal throughput
Total transport throughput must be equal to the
total assembly throughput
[math] T_T = T_A [/math]
Total transport throughput is product-volume times time-per-that-volume.
This time is transport-speed per chamber-sidelength (assuming cube shaped chambers with equal sidelengths):
[math] T_T = V (v_T/(sF)) [/math]
Total assembly throughput is layer-number n times product-volume V per the-time-that-it-takes-for-assembly-of-that.
This time is assembly-speed per total-motion-length of assembly of one volume V.
This total-motion-length is the chamber-sidelength sF times the number-of-parts B^3 times some factor C that is close to 1.
[math] T_A = n V (v_A/(B^3sFC)) [/math]
Now equating the two and simplifying we get:
[math] v_T = n v_A/(B^3C) [/math]
[math] v_A = v_T B^3 C / n [/math]
Discussion of preliminary result:
For one single layer n=1 assembly motions are B³C times faster than transport motions.
For n=B³C assemly motions are the same speed as transport motions.
The chamber to part size ratio F falls out of the equations.
Determining layernumber of minimal friction
Transport friction losses:
[math] P_T = \gamma (n A_T) v_T^2 [/math]
Assembly friction losses:
[math] P_A = \gamma (n A_A) (v_A)^2 [/math]
[math] P_A = \gamma (n A_A) ((v_T B^3 C)/n)^2 [/math]
[math] P_A = \gamma A_A v_T^2 B^6 C^2 / n [/math]
Total friction losses are comprised of transport & assembly losses:
[math] P_{total} = \gamma \sum_i A_i v_i^2 [/math]
[math] P_{total} = (A_T v_T^2 + A_A v_A^2) n \gamma [/math]
[math] P_{total} = \gamma v_T^2 (n A_T + A_A B^6 C^2/n) [/math]
Taking the derivative with respect to layernumber to find a the minimum for the friction losses:
[math] d P_{total} / d n = \gamma v_T^2 (A_T - A_A B^6 C^2/n_{opt}^2) = 0[/math]
[math] A_T = A_A B^6 C^2/n_{opt}^2 [/math]
And finally we get:
[math] n_{opt} = \sqrt{A_A/A_T} B^3 C [/math]
Side-note:
Transport bearing area A_T needs to cover both transport in and transport out,
since we did not consider these separately.
Collary:
Substituting that optimal layer into the expression for the assembly speed we get:
[math] v_{A,opt} = \sqrt{A_T/A_A} v_T [/math]
Determining layernumber of equal friction
No we ask for the transport losses to equal the assembly losses:
[math] A_T v_T^2 = A_A v_A^2 [/math]
Substituting v_a with our result for v_T:
[math] A_T = A_A B^6 C^2/n_{eq}^2 [/math]
And finally we get:
[math] n_{eq} = \sqrt{A_A/A_T} B^3 C [/math]
Analysis of result
Turns out this that ...
- the layermumber of equal friction coincides with
- the layernumber of minimal friction.
At this layernumber friction is minimal.
At this layernumber frictive losses from transport motions make up 50% of all frictive losses.
With more layers friction losses from transport motions grow linearly thwarting any further gains.
Interestingly (and perhaps quite unexpectedly) the ratio of the bearing areas goes in as a root.
Example
Wildly (but not totally unreasonably) assuming all factors but B are near 1:
This means:
- B=32 => n_opt=32768 layers.
- B=10 => n_opt=1000 layers.
This is a very favorable/convenient result.
(TODO: Check where the proposed speeds af ~5mm/s for nanofactories lie on the P_total(n) curve.)
Legend/Key for the variables
- n … number of layers (these are equivalently sized sub-layers, not to confuse with assembly layers in convergent assembly)
- V … product volume
- s … product sidelength
- sF … chamber sidelength
- F … chamber to part size ratio
- B … branching factor
- gamma … dynamic friction coefficient
- v_A … assembly speed
- T_A … assembly throughput
- A_A … bearing area per assembly unit
- v_T … transport speed
- T_T … transport throughput
- A_T … bearing area per transport track passing one assembly unit
- X … constant proportional to total throughput T
Concerns about input side transport bearing area (and friction)
For taking into account the bearing area of input side transport
one may assume a factor two in bearing area which goes in by its root.
BUT: Is the assumption of
"same bearing area at the input transport side as on the output transport side"
justifiable even though on the input side there are so B³ times more parts to transport?
Is seems yes. Efficient batch transport should be possible.
Wide attachment chains can transport many parts simultaneously.
For transporting a 3D volume options include at least:
- plates standing off from attachment chains
- transportation of parts magazines
Ingress and egress form the transport input-track can be counted to the
former layers output and this layers assembly chambers respectively.
Such a design calls for considerable additional design effort though.
Early developers may not be aware of the results derived here.
And only figure out this bottleneck in retrospect.
Thus for early systems the assumption of
"equal beating area for the input transport"
may me flawed due to the systems being far from optimal.
This may ask for rerunning this pages math with some modifications.
Furthermore
What about molecular assembly lines?
Basically one just simply replaces the assembly chamber column
in the middle between input transport and output transport by a column of.
one operation assembly line stations (mill style manipulators) that run
at the same speed as the transport motions.
To assemble a product out of B³ parts there naturally need to be n=B³ one operation assembly line stations
TADAAA that was surprisingly easy.
Changes a bit with operations that apply more parts (like carbon dimers).
Side-note: Mill style assembly is especially advantageous for the lowest assembly levels like
- Assembly level 1, molecular mills and before in
- Preprocessing step 2, tooltip preparation zone and maybe even before in
- Preprocessing step 1, molecular sorting zone, molecular sorting rotors (See: Acetylene sorting pump)
What about routing layers?
Note that the routing layers (at the output-side of assembly levels) are not treated here. Treated here are just the transport channels feeding parts in
- from the routing layers of the previous assembly level
- to the routing layers of this assembly level
This seems reasonable since the thicknesses of routing layers and
their internal operation speed will not change when the number of sub-layers is changed.
It may give a non negligible consant factor friction contribution though.
(TODO: Deeper investigation on routing layer friction losses needed.)
Math – relating to the compenslow design parameter
We want to keep the total throughput constant while tuning the compenslow parameter to reduce frictive losses.
To that end we assume that the layer number times the assembly speed is constant. This should be intuitively clear.
Halving the speed while doubling the amount of machinery (or vice versa) the throughput stays constant.
So we assume:
[math] n v_A = X = const[/math]
Substituting assembly the assembly-speed in the formula for the assembly throughput we get:
[math] T_A = V (X/(B^3sFC)) [/math]
Assuming constant T_A these are all constants.
Confirming our assumption that our introduced condition will cause that.
[math] X = T_A (B^3 s F C / V) = n v_A [/math]
(wiki-TODO: Relate X somehow to the compenslow quantities (chip area comes in too then))
Are there alternate limits?
What stops further increasing of layer-number to reduce friction further?
There are two cases:
- friction starts going up again due to transport motions becoming the dominant friction contributor
- there is just no more space for adding further layers of machinery without making the nanofactory chip into a skyscraper
There is no running out of space for nanomachinery due to its extreme throughput-density
Exploiting lower friction despite higher bearing area
in gem-gum factories is possible because very little volume of productive namomachinery
can already produce practical levels of throughput due to higher throughput of smaller machinery.
THUS: For the case of gem-gum factories (e.g. Assembly level 2)
hitting the "limits to lower friction despite higher bearing area" happens long before running out of space for more nanomachinery.
It's roughly B³ layers as we've seen.
Exception to the rule
Micromachinery to mesomachinery (in a stack of convergent assembly) is no longer nanoscale and thus it also no longer
benefits as strongly form higher throughput of smaller machinery
That is: For higher assembly levels with bigger assemby chambers it is likely to run into
limits to machinery parallelism due to space constraints rather than crossing the minimum of friction.
This suboptimality of the upper assembly levels is likely not relevant though
since the total contribution to frictive losses of the upper assembly layers is minute compadet to the losses from the lower assembly layers.
This is not due to lower bearing area (which is suboptimal as we've discussed)
but is rather due to the situation that friction in micro- to mesoscale bearings will
likely go up less severely with speed.
As we know is the case from today macroscale bearings.
See: Atomically precise roller gearbearing
Very important note
It may be possible to significantly reduce bearing area in transport channels relative to bearing area in assembly chambers.
As attachment chains can run through free and empty space if no forces are applied.
Only the very ends need of the attachment chains need to be supported by sprockets.
This means the optimal layer-number where friction per throughput gets minimal may go up by a significant margin.
That is by several decimal orders of magnitude!!
Related
- Sub-layer
- Nanofactory math based on continuity of throughput … within assembly levels and across assembly levels
Compenslow:
Tuning layer number n assembly speed v_A such that throughput stays constant
is identical to changing the compenslow design parameter.
External links
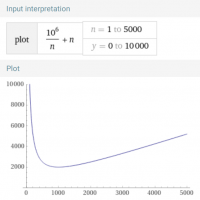
Qualitative shape of friction-losses plotted over layer-number:
plot(10^6/n+n,n,1,5*10^3) (on wolfram alpha)
