Difference between revisions of "Circumsembly"

Revision as of 20:21, 18 November 2024

A semi-conceptual illustration visualizing fault tolerance in selfassembly (at first and second assembly level) enabled by provision of parallel pathways for the completion of still missing areas of self-assembly. – 3D voxel block structural DNA nanotechnology used as inspiring example.

Circumsembly (or redundant access self-assembly) is selfassembly where
different parts A and B of the product-to-self-assemble are reachable by n (n being at least two) possible pathways, such that
if up to (n-1) paths between A & B are blocked by irreversible assembly errors, self-assembly can still proceed from A all the way to B.
In practice much less than (n-1) paths should ever be blocked and the wole product assembled. Minus the few irreversible assembly errors which can be tolerated in a good design.
(wiki-TODO: add a sketch)

(Choice of name: "circum" from circumventing assembly errors.)

Relation to yield in the synthesis of chain molecules

artificial synthesis of chain molecules by iterative addition of monomers to the reactive end
suffers from exponential/geometric drop-off in yield.
With every added monomer a probability smaller one of failure is multiplied.

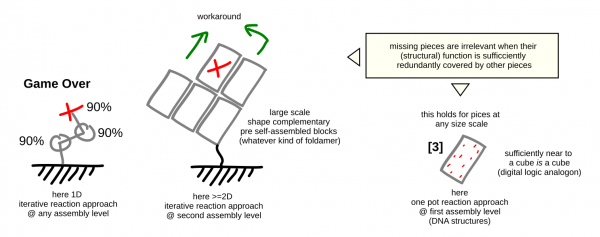
An artificial selfassembled rod of de-novo proteins can suffer the same.
But a stiff rod made from several parallel sub-strands can circumvent irreversible errors.

Prerequisites for circumsembly

• selfassembly at multiple spots simultaneously
• sideward assembly crossing sub-strands is possible
• sufficient stiffness of selfassemblies such that the same spot can be reached via multiple (at least two) pathways

Benefits of circumsembly

• A much reduced dropoff in yield of product.
  Especially for 2d and 3D structures where the number of paths for circumvention grows quadratically/cubically respectively.

The math for how the drop-off in yield is reduced exactly in not entirely nontrivial.
(wiki-TODO: check out the math more closely) Minimal problem:

• Given A rod of n parallel rows of 2D-squares starting out empty adding to the right only.
• Successive addition at the growth front – this needs to accounting for sideward additions – nontrivial
• What is the average blocknumber till all paths are blocked

This is likely easy for n=2 analytically.
For bigger n this might be easiest answered with a simulation.

Related

• termination control
• squigglesembly
• de-novo proteins
• steric traps

• Persistence length