How do atoms work?

The common symbolic depiction of atoms with lines for orbits and little balls on those lines for electrons and further little balls for the protons and neutrons in the core is awfully bad and very far from the real situation.

Atoms are mostly electrons by volume. Soft electron density clouds. No empty space.

A decent intuitive picture for atoms are soft/blurry clouds that are (in a certain mathematical sense) as smooth as possible and can exert soft forces on other of these clouds in case they come close. There are no hard surfaces and certainly no sharp planet like orbits. These clouds are made of so called "electron density". Atoms basically are electrons. The electrons in atoms (especially the outermost ones) not just have the size of atoms they literally are the atoms. The nucleus of an atom gives it basically just its mass (which is almost irrelevant at the nanoscale). And sometimes weak magnetic properties that can in the context of mechanosynthesis be ignored.

Electrons in solids can occupy a space that is much bigger than an atom. As an example: Free electrons in metals are of such nature.

Electrons density clouds in atoms can not be smaller than the innermost electron shell.
This is partly because of a see-saw effect that:

makes tightly constrained electrons move more vigorously and that
makes electrons with a very precise temperature (very cold is easiest) very big

This see-saw effect is called the "Heisenberg uncertainty relationship".
Where it exactly equilibrates out is determined by the Schrödinger equation.

Beside the electron density cloud interpretation there is also the probability density cloud interpretation.
While useful mathematically the author of this wiki is not a fan.
See "on the probability interpretation of quantum mechanics" for details. Warning this gets a bit technical.

Only because electrons are forced to "stack" on each other directed chemical bonds exist.

The very small core/nucleus of the atom (which btw is also cloudy but more rowdy - excuse the joke) just serves as a very well hidden electrostatic "glue" holding the electron cloud together. The inner electrons serve as padding. Due to the Pauli exclusion principle they inner electrons blow additional electrons further up making them stick out the farthest and thus making them the so called "outer shell electrons". Only due to this outward shifting the outermost exposed electrons undergo interesting changes that make chemical bonds possible.

What kind of interesting changes?

Atoms are just like drums ... with lots of exceptions.

A demo experiment showing a so called "Caldni figure". The sand collects where the plate moves the least up and down. At the vibration nodes. In the atom analogy the black areas between the nodes are the spots where the electron clouds are densest. The orbitals.

As a first crude starting analogy imagine the electron density (actually a precursor of it) as the skin on a drum. The lowest tone you can play makes the whole membrane go up and down (a single antinode of vibration).

There are several points where the useful drum analogy breaks and some awkward peculiarities show up:

The membrane has no border – (again: there are no sharp surfaces).
The tension of the membrane changes towards the center.
The membrane is not two dimensional but three dimensional and it does not swing up and down but into a further dimension that is the precursor of electron density. This precursor can be best expressed with complex numbers and is called the "wave function" of the electron.
Every tone can be played at exactly one volume.
Every tone can be played exactly twice (spin up and spin down) then if one wants to play more tones one needs to go on to the tone next higher in frequency/pitch or to a tone different in geometry. (This is due to the Pauli exclusion principle.)
Tones do not radiate away energy. They do not emit the equivalent of the drum-analogy-soundwaves in form of lightwaves. Instead they stay at their frequency pitch permanently unless actively driven away. Electrons don't "fall" into the core due to the seesaw that makes electrons move more vigorously when they become tightly constrained in space. The "heisenberg uncertainty relationship".
The overtone vibration geometries have inter-dependencies (more on that later).

(Related: Analogies and their dangers)

Once the first shell is full the next electrons go in next hull with one more node

Exactly two electrons go into the very first tone (the two spins - spin up and spin down - then this place is full - Pauli exclusion). The next higher tone of the drum (aka the first overtone) has the inner circular area of the drum going up-then-down and the outer circular ring-area going down-then-up. In the 2D drum model a motionless circular "nodal line of vibration" is located between the two "antinodes of vibration". In the real 3D atom this "node of vibration" is a theoretical infinitely sharp spherical shell with the inner and outer volume separated by this shell swinging complementary to each other (in antiphase).

Technical side-notes: The number of nodes can further rise and directly corresponds to the strain and energy in the "drum membrane" (curvature in the wave function). With every additional node one is raising up one energy level. These energy levels are characterized by the "main/principal quantum number" with symbol "n". Numbers of n have associated letters (0=k 1=l 2=m ...).

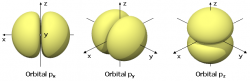
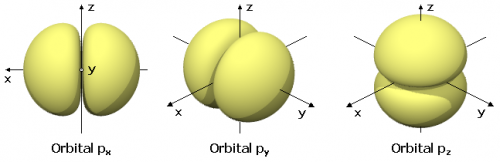
Beside sphere shaped nodes there can be two other shapes of nodes

The simplest non spherical nodal surface is one flat nodal surface: Depicted here are the two volumes containing the antinodes of such a single flat nodal plane (p-orbitals).

There are overtones with non-spherical nodal surfaces too. In the 2D drum model imagine the left side of the drum going up-then-down and the right side going down-then-up. It's a bit more complicated in 3D atoms though.

There are nodal surfaces that have the shape of nested double cones (and one plane in case of even node-surface numbers) dividing the wave function in one double lobe and some rings. (Rings only if there's more than one node-surface.)
There are nodal surfaces that are all flat planes which divide the wave function into orange slice shaped antinodes.

The former is described by the "secondary quantum number" with symbol "l". Again numbers of l have associated letters (1=s 2=p 3=d 4=f). The latter is described by the "magnetic quantum number" with symbol "m"

With more radial nodes the number of possible nodes of other type grows

Due to the fact that the wave functions are a result of a certain very famous differential equation there are some relations between those so called "quantum numbers". These relations are: (n>0; l<n; abs(m)<=l). In words: higher overtones (vibrational modes) of different kind than spherical only become available when the energy rises above the minimum (n>1).

Nodes can be shifted from one type to another. Every combo adds space for electrons in a single shell.

Note that when n becomes 2 then l can be lifted from 0 to 1. This lifting drags the spherical/radial node-surface over to a conical node-surface. The spherical node-surface is gone (kind of like a conversion). Also one can further "lift" m form 0 to minus 1 or plus 1. This further drags the conical node-surfaces over to a planar node (again kind of like a conversion). Now the conical node is gone too. With higher n one can leave some spherical/radial node-surfaces behind albeit converting some to the conical type and one can leave some conical ones behind albeit converting some to the planar type. This allows for complex patterns (technical term "spherical harmonics"). We are especially interested in the volume-slivers between the node-surfaces. These are the basis for orbitals bonds and the shape of molecules. But we are not quite there yet.

The order the electrons fill the shells can be complicated. It is strongly environment dependent.

Technical side-note: There are the so called "Hund's rules" describing in which order electrons fill up the quantum numbers. This though applies only for unbond atoms that freely float in vacuum (E.g. found in vaporized metals in gas discharge lamps. Lamps that where and still are very useful in fundamental physics.) Since in the context of APM we are mostly interested strongly bonded atoms these rules are not useful as they are. Instead the described vibrational modes of the wave function combine in other more or less nontrivial ways to bonding orbitals such that energy is minimized.

What kind of shape do atoms have?

Now with the somewhat intuitive drum analogy for the oscillating wave function and the vibrational overtones of the wave function which are dividing atoms into kind of a 3D checkerboard pattern (spherical harmonics) we are slowly beginning to get some structure that we'll need to form directed chemical bonds.

Our goal is to get directed lobes (bonding electron orbitals) from the nodes in the wave function but there is another not yet mentioned peculiarity which makes getting bonding orbitals from the basic patterns more difficult for us.

The problem is that electrons can not only oscillate they can also rotate (since there's no angular constraint - no "wall" in the atom). The density of a moving/streaming/rotating one electron cloud (both linear and like in our case circular) features no nodes. This is because:

The precursor of the electron density(the wave function) has its purely complex part phase shifted relative to the purely real part in the direction of movement - (TODO: check sign). Side-note: From the shift in the wave function one can derive the direction of motion even when given only a momentary snapshot, so the shift can be seen as the encoding of the motion. The motion is the shift so to say. It's one and the same.
The density of the electron cloud is obtained from the wave function by forming the "square of the absolute value".
The resulting density of this moving phase shifted wave functions is constant and nowhere zero.

So none of the nodes and antinodes of the wave function make it over to the electron density. We don't get the desired patterns of slivers between nodes-surfaces that are bonding orbitals.

Side-note: Despite the many vibrational node-surfaces, free atoms that are floating around in a vacuum (and that are not under the influence of magnetic or electric fields) have the shape of perfect spheres when the wave function is converted to observable electron density. This is exactly because they have no rotational constraints. (Related: symmetry <=> conserved quantity == Nöther theorem)

While the p_z orbital is a direct result of the Schrödinger equation (for an electron in the potential of a nucleus) the p_x and p_y orbitals are not. For the p_x and p_y orbitals two counterclockwise rotation solutions (rotating in complex number space) need to be added such that the associated electron density gains lobes. The phase in which the solutions are added relative to one another determines the direction in which the resulting orbitals will face in the x-y plane.

To get patterns one can reflect back a one electron stream on a wall into itself or as in our case we can add fractions of the one electron stream rotating backwards (this is a quantum superposition btw) some parts of the wave function cancel out (self interference) and after applying the "square of the absolute value" to get our (observable) electron density we finally get lobes (we have standing waves).

Looking backward when one has (at least one) chemical bond to something non rotation (e.g. a macroscale slab of crystal) this bond could be seen as the aforementioned "wall in the atom" that prevents rotation.

To minimize energy furthermore the basic wave functions are combined in such a way that energy is minimized (metastability not considered here). From that one gets various combinations of basic orbitals which are called "hybrid orbitals". The most important hybrid orbitals for the lighter elements are the called sp³ and sp². There's also the more rare sp hybridization.

sp³ orbitals

Tetrahedral geometry of sp³ hybrid orbitals. Note: Simplified view! Actual orbitals: more bean shaped and overlapping.

sp³ hybridization results in four strongly asymmetric double lobes oriented in tetrahedral geometry. The shape of coastal defense tetrapods. The small sides of the lobes are hidden away in the atoms inner shells.

The orbitals of atoms facing one another bond big lobe facing big lobe. These bonds are so called "sigma bonds". A classic example for a solid material featuring sp³ bonding is diamond. Note that one needs at least four bonds not lying in a common plane such that one can create densely meshed 3D structures that are not just folded chains or sheets. A classic example for a volatile compound featuring sp³ bonding is methane CH₄

sp² orbitals

Triangular geometry of sp² hybrid orbitals. The fourth orbital (the p-orbital facing in and out of the image plane) is not depicted! Note: Simplified view! Actual orbitals: more bean shaped and overlapping.

sp² hybridization leaves one p orbital (p_z) intact (as it is) the remaining three are converted in asymmetric double lobes (less strongly asymmetric than sp³). The small sides of the lobes are hidden away in the atoms inner shells. The remnant symmetric p_z orbital is oriented vertically while the three sp² orbitals lie in a normal plane forming an equilateral triangle.

The hybridized orbitals form again form sigma bonds. Actually the unaltered p_z orbital are more interesting here. Double lobes bond sideways to other double lobes making single bonds with two contact points so called "pi bonds". A classic example for sp² bonding is: graphite, nanotubes, buckyballs, ...
Depending on bonding topology and lattice strain the electronic properties of these pi bonds can be tuned in a very wide range. From metallic over semi-metallic to non metallic.

Two extreme representations of a carbon-carbon double-bond. The "real" situation lies inbetween. Left: an sp² sigma-bond combined with a two pronged pi-bond (unhybridized double-lobed p_z orbital). Right: two highly bent/strained sp³ sigma bonds.

Note that hybridization is not clearly classifiable into the three categories sp³, sp² and sp. It is more like sp^λ where λ can be a fractional number. A continuum. After all, hybrid orbitals are just a mixture (more accurately a "linear combination") of orbitals where any combination can be assumed (as long as electron density adds up to one - normed integral). What ever minimizes energy most will be assumed. (In molecules the λ value can be experimentally deduced from the angles of the hydrogen atoms sticking out.)

Note that bigger atoms with the "same" electron configuration in the outer shell (sitting below carbon in the periodic table) like e.g. silicon, and germanium rarely form sp² or sp bonds. It's not fundamentally impossible but these bonds are very unstable. The inner electrons are in the way.

sp orbitals

Linear geometry of sp¹ hybrid orbitals. Two missing orbitals (two p-orbitals - both oriented normal to all others) are not depicted! Note: Simplified view! Actual orbitals: more bean shaped and overlapping.

sp hybridization leaves two p like orbitals intact (rotation compensated - as noted above) the remaining two are converted in asymmetric double lobes (less strongly asymmetric than sp2). The small sides of the lobes are hidden away in the atoms inner shells. The two remnant symmetric p like orbitals are oriented normal to each other while the two sp orbitals stick out on opposite sides of the formed cross. Attention! these two can be mistaken for a unmodified p orbital.

sp hybridization occurs in the gaseous compound ethyne (C₂H₂) aka acetylene aka welding gas. This gas is of especial interest for advanced mechanosynthesis of diamond because a triple bond between two carbon atoms leaves just two bonds capped with hydrogen. When assembling something like a block of diamond instead of hydrocarbon chains there is very little surface area and all that excessive hydrogen would need to be reacted to water leading to a massive energy excess.

d and f orbitals and their hybridization

TODO ...

Notes

Going down backwards one finds:

angular part: Spherical harmonics, associated Legendre functions, Legendre polynomials
radial part: Laguerre polynomials
Schrödinger equation – separation of variables => radial part and angular part

Exact solutions exist only for the hydrogen atom (and one electron ions). As soon as there is more than one electron mutual electrostatic repulsion drastically changes the results. Exact solutions are no longer possible. There are iterative approximation methods. An important basic one among them is the "Gram–Schmidt process".

Spherical harmonics are often depicted as surfaces where the magnitude value is misused as radius. These (tear shaped) plots can be easily confused with molecular orbitals (bean shaped). But molecular orbitals are constant value surfaces of the square of the absolute value of the spherical harmonic angular part of the wave function multiplied by the radial part of the wave function. When hand drawn molecular orbitals often are drawn tear shaped.

External links

"Orbital Viewer" by David Manthey (Windows program - but it runs perfectly fine under wine in linux too)
The Shapes Of Hydrogen - Poster ... by DarkSilverflame (deviantart)
Common question: Does an atom mostly consist of empty space? (No.)

Wikipedia

The crude drum analogy: Ernst_Chladni#Chladni_figures (de) – Analog to two dimensional vibration node planes in three dimensional atoms there are one dimensional vibration node lines on two dimensional oscillating surfaces. The details are vastly different though.

The simplemost way to combine multiple orbitals is just adding them up.
This must be done before(!!) taking the square of the absolute value.
This trivial method goes under the fancy name of: LCAO linear combination of atomic orbitals.
Only the orbitals of hydrogen like atoms are describable by "simple" (meaning analytically closed) mathematical formulas. Even rather simple multi electron atoms (like carbon) have a complex charge distribution of electrons added upon the simple point charge of the nucleus. This makes the energy potential V nontrivial. And this in turn leads to the necessity of iterative approximation methods.
This challenging problem is called the shielding effect. It is present in all multi electron atoms (all uncharged atoms except hydrogen). The simplemost but very inaccurate form of treating it is via an effective nuclear charge. Much better is to use a modified potential that deviates from "~1/r²". The potential can be iteratively adjusted too. Until the potential matches the wave function and vice versa (that is until so called "self consistency" is sufficiently archived).
(TODO: start iteration with ~1/r² potential or other one?)
Iterative approximation methods: Gram–Schmidt process; Hartree–Fock method; Born–Oppenheimer approximation
(TODO: There is a basic iteration method to fit a initially guessed wave function to a slightly modified potential. How is this method called again?)

The nature and shape of atoms

Contents