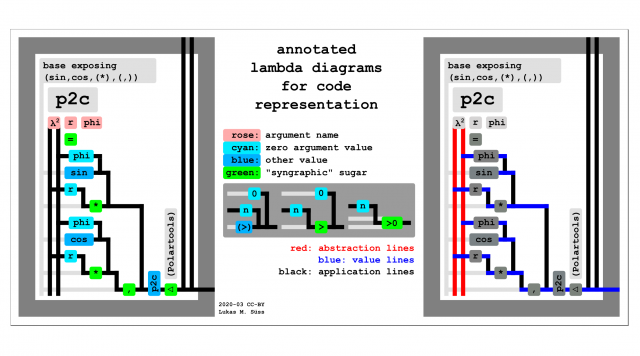
Syngraphic sugar
"Syngrahphic sugar" shall here mean "syntactic sugar" but for "graphical syntax" as found in annotated lambda diagrams.
As of (2021) "Syntatctic sugar" is an established term in the context of functional programming (see in external links and ....)
Wikipedia about syntactic sugar:
"In computer science, syntactic sugar is syntax within a programming language that is designed to make things easier to read or to express.
It makes the language "sweeter" for human use: things can be expressed more clearly, more concisely, or in an alternative style that some may prefer."
Contents
[hide]Concrete examples
Syngraphic sugar in annotated lambda diagrams
Annotated lambda diagrams without any "syngraphic sugar" enforce prefix notation for functions with two arguments (2ary functions).
That is e.g. one must write:
- (> n 0) instead of (n > 0)
- (+ 1 2) instead of (1 + 2)
- (* r (sin phi)) instead of (r * (sin phi))
Well; The visual equivalent of that.
Syngrahic sugar is marked bright green in the image on the right.
Example: (n > 0) ⇒ (> n 0) ⇒ n (>0)
For the example (n > 0) in visual style see center of the image on the right.
With (n > 0) represented in three annotated lambda diagram styles
that increasingly add the amount of "syngraphic sugar" from left to right.
First: The (>) label is shifted to the right.
Putting the "value-annotation-label" of a "value-line"
(dark grey boxed on blue horizontal lines in graphic on the right respectively)
Deliberately between the application of arguments (which is type incorrect) like that
can make reading more natural and easy.
Second: The comparison with the constant number 0 is subsumed in the "syngraphic sugar" too.
As it is done in pretty much all programming languages.
Actually the feature of (optionally) removing syntactic sugar to sucha a degree might be quite unique to annotated lambda diagrams.
Something interesting happens when:
- adding types to plain lambda diagrams and
- cutting them up into composable standalone pieces.
Going down the tree of computation from several inputs to one single output
(always the case because that's part of the definition of a function in the mathematical sense) , the types all match up.
But the final result type (a pair of cartesian coordinates in the example) does not match with the incoming argument types
(long vertical black "application lines" on the right)
What the incoming argument types require is a a function from radius and angle to a pair of cartesian coordinates. Not just a pair of cartesian coordinates.
To visualize that rift in type (that gets resolved during evaluation) the "finalization marker" (here a left facing hollow triangle) is added as syngraphic sugar.
The reason for the type rift (and thus this marker being necessary) seems to be that in lambda diagrams abstraction and application are
not yet short circuited at whenever new "abstraction lines" (red vertical lines in the graphic) appear.
Cases where new abstraction lines appear include
- top of all functions (or more precisely crossing borders of closures) – except "magic" functions that take no arguments
- let ... in ... constructs within closures
Syntactic sugar in the function header of annotated lambda diagrams
The equal sign (as present in the p2c example here) is pretty much pointless.
It is just here to make the code look more like normal textual code.
And make entry with pre-existing programming knowledge more pleasant.
The lambda marker is similarly optional. It can be omitted too. It is maybe a bit more useful though.
It gives a redundant hint that what follows are function argument(s)
(and a hint on that these can be interpreted as a lambda calculus abstraction)
The superscript on the upper right denotes the number of arguments.
The number of arguments is written as a power since a function corresponds to potentiation in the category theoretic analogy.
It's still only symbolic though since various argument types cab be mixed together here.
In case the arguments are not collected into one line (like done so in plain lambda diagrams) but instead
spread out ober multiple lines (e.g. to make space for long variable names and exposed types) then
each line gets a lambda with a power of one</small>.
A lambda marker with a power of zero is basically only present for "functions" withount arguments aka constants that are solely composed of implicit (and also constant as all content addressed library content) library dependencies.
Further cases of syngraphic sugar in annotated lambda diagrams
- Visualization of the arity of a value
- Extraction of head and tail from a list
- let ... in ... constructs
- case ... of ... constructs – there's more to tell here ...
- ...
Syntactic sugar in textual programming
Example: syntactic sugar replacing brackets
- def f (a, b, c, d, e): = a( b( c( d( e ) ) ) ) – in variations widely used syntax that is obfuscation the possibility of partial function application (currying) – python
- (defun f a b c d e) = a (b (c (d e))) – minimalistic (but possibly to verbose) syntax without syntactic sugar – lisp / scheme (((((infamous for the mountains of brackets)))))
- f a b c d e = a . b . c . d $ e – baroque (but possibly too cryptic) syntax with syntactic sugar – haskell
Actually the haskell example here may not classify as syntactic sugar since (.) and ($) are both implemented from within the language itself.
Functional programming syntax that is using and placing brackets very differently to mainstream imperative programming
can be unnatural if one is not used to it.
Usage of brackets in the mainstream programming way is usually not classified as syntactic sugar
since syntactic sugar is supposed to make working easier not harder.
Notes
Syntactic (and syngraphic) sugar can be:
- cryptic if too much of it is introduced at once – can be an undesired barrier to entry
- cryptic if too much of too terse forms are used – a barrier for all programmers that are humans rather than computers
- if used inappropriately more visually obfuscating than elucidating – this is depending on the situation of course.
- once picked only changeable in a limited way (depends on the programming language)
When it comes to syntactic sugar programming languages may allow some flexibility. But typically only to a degree.
Beyond that they come with their "poison to pick" and stick with. At last all mainstream languages of today (2021).
To avoid getting trapped by a particular type of syntactic sugar:
- With code projection there is no no need to commit to a specific style anymore.
This can come with a loss of syntax irrelevant formatting choices like indentation styles though.
To clear up potential misconceptions:
- Code projection does not not necessarily mean structured editing
- Structured editing does not not necessarily mean that "typing normally" cannot be supported
An important basis:
- A content addressed approach on codebases should massively help in implementation of languages capable code projection