Syngraphic sugar
"Syngrahphic sugar" shall here mean "syntactic sugar" but for "graphical syntax" as found in annotated lambda diagrams.
As of (2021) "Syntatctic sugar" is an established term in the context of finctional programming see in external links and ....
Wikipedia about syntactic sugar:
"In computer science, syntactic sugar is syntax within a programming language that is designed to make things easier to read or to express. It makes the language "sweeter" for human use: things can be expressed more clearly, more concisely, or in an alternative style that some may prefer."
Contents
Concrete examples
Syntactic sugar in textual proggramming
An example of syntactic sugar may well be lisp/scheme
- def f (a, b, c, d, e): = a( b( c( d( e ) ) ) ) – in variations widely used syntax that is obfuscation the possibility of currying – Python
- (defun f a b c d e) = a (b (c (d e))) – minimalistic (but possibly to verbose) syntax without syntactic sugar – lisp/scheme (((((infamous for the mountains of brackets)))))
- f a b c d e = a . b . c . d $ e – baroque (but possibly too cryptic) syntax with syntactic sugar – haskell
When it comes to syntactic sugar programming languages may allow some flexibility but only to a degree.
Beyond that they come with their "poison to pick" and stick with.
Syntactic (and syngraphic) sugar can be:
- quite unnatural if one is not used to it or even
- more visually obfuscating (depending on the situation).
Well some notes are in order ...
- With code projection there is no no need to commit to a specific style anymore.
This can come with a loss of syntax irrelevant formatting choices like indentation styles though.
- Code projection does not not necessarily mean structured editing
- Structured editing does not not necessarily mean that "typing normally" cannot be supported
- A content addressed approach on codebases should massively help in implementation of languages capable code projection
Syngraphic sugar in annotated lambda diagrams
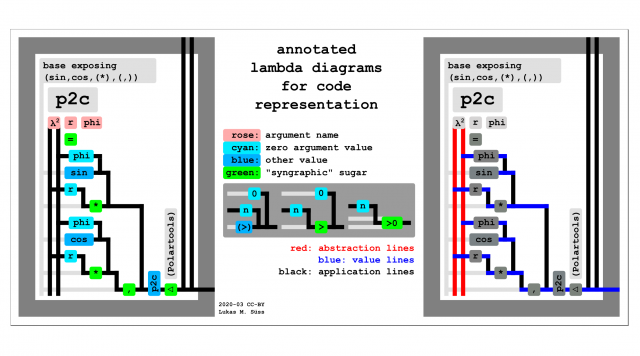
For details see: ALDs – example Cartesian to polar.
Annotated lambda diagrams without any "syngraphic sugar" enforce prefix notation for functions with two arguments (2ary functions).
That is e.g. one must write:
- (> n 0) instead of (n > 0)
- (+ 1 2) instead of (1 + 2)
- (* r (sin phi)) instead of (r * (sin phi))
Well; The visual equivalent of that.
Syngrahic sugar is marked bright green in the image on the right.
Example: ~ (n > 0) ~ (> n 0) ~ n (>0)
For the example (n > 0) in visual style see center of the image on the right.
With (n > 0) represented in three annotated lambda diagram styles
that increasing add the amount of "syngraphic sugar" from left to right.
First: The (>) label is shifted to the right.
Putting the "value-annotation-label" of a "value-line"
(dark grey boxed on blue horizontal lines in graphic on the right respectively)
Deliberately between the application of arguments (which is type incorrect) like that
can make reading more natural and easy.
Second: The comparison with the constant number 0 is subsumed in the "syngraphic sugar" too.
As it is done in pretty much all programming languages.
Actually the feature of (optionally) removing syntactic sugar to sucha a degree might be quite unique to annotated lambda diagrams.
Something interesting happens when:
- adding types to plain lambda diagrams and
- cutting them up into composable standalone pieces.
Going down the tree of computation from several inputs to one single output
(always the case because that's part of the definition of a function in the mathematical sense) , the types all match up.
But the final result type (a pair of cartesian coordinates in the example) does not match with the incoming argument types
(long vertical black "application lines" on the right)
What the incoming argument types require is a a function from radius and angle to a pair of cartesian coordinates. Not just a pair of cartesian coordinates.
To visualize that rift in type (that gets resolved during evaluation) the "finalization marker" (here a left facing hollow triangle) is added as syngraphic sugar.
The reason for the type rift (and thus this marker being necessary) seems to be that in lambda diagrams abstraction and application are
not yet short circuited at whenever new "abstraction lines" (red vertical lines in the graphic) appear.
Cases where new abstraction lines appear include
- top of all functions (or more precisely crossing borders of closures) – except "magic" functions that take no arguments
- let ... in ... constructs within closures
Further cases of syngraphic sugar in annotated lambda diagrams
- Visualization of the arity of a value
- Extraction of head and tail from a list
- let ... in ... constructs
- case ... of ... constructs – there's more to tell here ...
- ...