Typed holes
Typed holes can be used for:
- automatic suggestion of matching functions (depending on context)
- treating fragments of code like fragments of a (drag and drop) jigsaw puzzle with comparable seams
- storing partially complete programs in the codebase (serves as TODO documentation)
- shifting around type mismatches to where they are relevant rather where they are auto-detected by forward or backward type inference
- seeing intersections of type-class constraints
- combining edit-time, compile-time, and run-time simultaneously in a (projectional/structural) coding interface
- having as much code as possible live (code flowing around obstructions in nonempty holes)
- ...
For some drag and drop of typed holes
see the annotated lambda diagram mockups
Contents
Local code fragments
Input hole - aka undefined argument
A local function with an argument lacking a link to an eventually needed dependency.
Collectively input holes define the input surface of a code fragment.
(The local functions needs to have at least the inputs already being defined).
Output hole - aka result
Output of a function that already got defined.
It may have zero or more use contexts already but
locally is not hooked up to anything yet.
Collectively output holes define the output surface of a code fragment.
(Multiple use of outputs calls for let…in constructs).
(The local functions needs to have at least the return type already being defined).
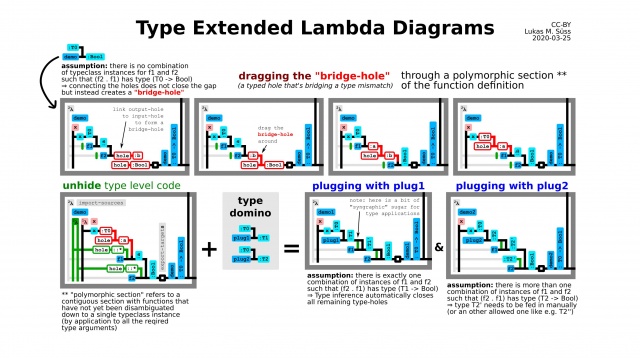
Bridge holes
Intended connection points with type mismatch.
Expression of programmer intent.
Eventually need to be filled either by a function or
by a whole program fragment bridging the type-gap.
Internally a code fragment can be partially connected
and feature complex gaps (many output and input holes).
Holes at the local functions contexts borders
Unused parameters – output holes
Parameters/arguments that are given to a function but then not used.
Use count is 0.
Undefined return value - input hole
There is "nothing" connected to the output of the function yet.
No code fragments to drag and drop
Code-fragments connected spanning across function borders
cannot be treated like drag and drop puzzle-pieces.
If that's desired the code should probably factored differently.
Code fracture as the dual to code fragment
When working from the function fringes inward then
maybe it is better to look at it inversely.
A code fracture splitting the void.
There is literally a void type.
More on that later.
Orthogonal hole properties
Typeclass-intersection holes
These carry constraints on types that do not yet narrow the type down to uniqueness.
Connecting output holed and input holes with different type-class constraints
gives an intersection of the constraints.
Non-empty holes
These carry both defined and undefined values within.
Both can flowing through.
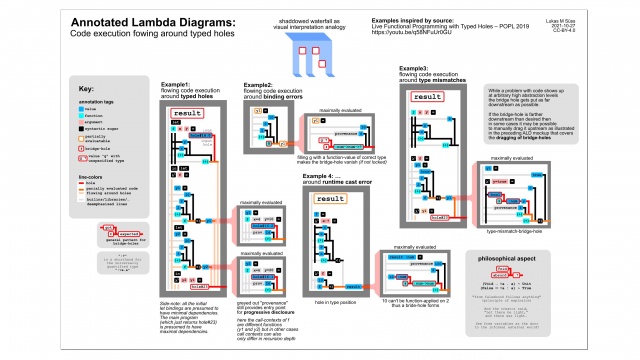 Nonempty holes illustrated using a mockup of annotated lambda diagrams. See also: Annotated lambda diagram mockups. |
Misc practical notes
Design decision to make:
Does/can the order of argument carrying meaning or not.
With types argument order can often be figured out by matching type.
Design decision to make:
Structural editors could even allow for generating arguments values and
return values without requiring a human readable name.
Automatic numbered names (hash).
But this seems questionable at best. Likely a quite bad idea.
– Human naming laziness may lead to unnamed variables remaining
– Dealing with the additional case of unnamed variables is then needed
Special types & philosophical aspects
Void
There is the special type Void representing Perhaps:
- most precisely: type with no inhabitants - aka bottom
- undefined ("undefined" it's kind of an inhabitant though looking at it from the meta level)
- non-terminating computation (we never get the result for sure)
- unknown whether or not terminating (may not be correct - to check)
The void type seems like the type describing the maximally undefined value.
As such it seems strongly related to typed holes.
To build up a program from nothing (blank canvas) one needs to
introduce axiomatic rules from nothing.
As such starting from void type seems natural.
From falsehood follows everything.
Means one can always spawn a function with corresponding types from nothing.
But better pick your programs axioms wisely!
One could perhaps say: As programmer you can play god of your own creation.
A void typed input hole can never be filled.
It looks like it matches with a void output hole but
connecting them is meaningless as it is equivalent to not connecting them.
What could perhaps be interpreted as function from void to value are
- hard-coded constants
- builtin functions
"Magic" entropy from the environment.
Possibly related to that:
- Type constructors => corecursive construction of algebraic datatypes
- Type deconstructors => recursive deconstruction of algebraic datatypes
Type deconstructors corresponds to pattern matching in case-of expression.
Unit
The special type Unit or () representing Perhaps:
- most precisely: type with exactly one inhabitant - aka top
- existence of the value carried by the type
The unit type seems to suggest itself for usage to force delayed computations (in lazy evaluation).
Not sure if that is proper usage. It seems not as evaluation strays from timeless denotative meaning.
Ignoring evaluation a unit type cannot transmit any information as it only has one state: ().
It only gives info about the existence "inhabitedness" of a final program evaluation result.
Just from this type alone as input nothing but the same unit type can be deduced.
Question
In an elegant (more discovered than invented) language what does the
topmost function (usually called main) must always have ad inputs and outputs?
Correspondences
- Types: "Void"
- Logic: False
- Category theory: "Initial Object" or 0
- Typed: () or "Unit"
- Logic: True
- Category theory: "Terminal Object" or 1
For more see: Curry-Howard-Lambeck isomorphism