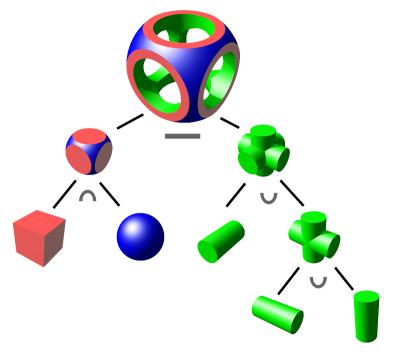Constructive solid geometry

From apm
Jump to: navigation, search
Constructive solid geometry

Constructive solid geometry (CSG) is a form of volumetric modelling where complex geometries can be built up by combining simple geometries via boolean functions.

F-Rep vs B-Rep

  • F-Rep … functional representations – implicit functions specifying a volume
    Signed distance functions SDFs are a subset.
  • B-rep … boundary representation – description of 2D surfaces in 3D space
    May be parametric, piecewise parametric, or even piecewise linear (aka triangulation)

Why functional representation is desirable

Functional representation (representing volumes with an implicit function in three variables) is especially suitable for CSG.
Functional representation (F-Rep)

  • is typically more robust than boundary representation (B-Rep)
  • is resolution preserving, and
  • the boolean operations can be combined with blending operations with a simple change in math.

Pro: Higher robustness

Functional representation is typically more robust than a triangulation based boundary representation.
There is no need to worry about

  • holes in meshes (meshes being not "watertight")
  • flipped normals, degenerate triangles, coaxial edges, and
  • a gazillion of other possible bad configurations.

Con: No convex hulls (general case)

Functional representation has one major weakness though:
The extremely useful of creating convex hulls seems not implementable (aside from a few special cases maybe)

F-Rep is higher level than piecewise linear B-Rep

Positive lobe of a p-orbital (single electron solution for the Schrödinger equation) this can be done via F-rep but not via SDF. Related Atomic orbitals.

Functional representation (F-Rep) is on a higher abstraction level than triangulation based boundary representation (B-Rep). That is

  • F-Rep can be triangulated to piecewise linear B-Rep to arbitrary precision
  • Going from B-Rep to F-rep requires a bit of artistic creativity filling in the blanks

The relation between F-rep and polygonal modelling B-rep is respectively a bit like:

In all three cases dragging out the discretionary step to the last possible moment is the way to go.
Manipulation of the continuous not jet discretized representations allows for more expressiveness and
even more importantly more scalability in the complexity of systems modeled.

SDF vs F-Rep

With signed distance functions (SDFs) ...

  • the value of the scalar field always represents the distance to the nearest surface
  • the magnitude of the gradient id always one

This ...

  • allows for much more efficient evaluations, surface can be found in one step rather than needing root finding algorithms
  • makes most volumes (beyond simple quadrics) hard to express or not expressible (e.g. atomic orbital isosurfaces)

F-Rep is more general than SDFs but slower to evaluate.

Why signed distance functions (SDFs) are desirable

Functional representations with their scalar field (f(x,y,z) in R3 aka "algebraic variety")
being constrained to a norm of one can be useful.
(a special case with magnitude of gradient always being one - and C0 continuity?)
Finding points on the surfaces (by some root finding algorithm like Newton method or Regula falsi) can be much faster (one step).
That is useful for:

  • Faster triangulation
  • Ray marching

As an example:

  • y^2 + y^2 + z^2 < R^2 – evaluated without taking toots suffices to define a sphere
  • sqrt(y^2 + y^2 + z^2) < R – evaluated this way unlocks the power of SDFs at the cost of needing to compute a root

F-Rep basics

Only a few types of elements are essential for F-Rep CSG

  • The base volumes
  • The boolean operations for combining them
  • The coordinate transformations
  • (projections)

For a convex hull over any geometry it seems
it is unavoidable to leave F-Rep and triangulate down to B-Rep

Base volumes

Volumes are defined just by implicit functions in 3 variables (f(x,y,z) in R3)

Boolean operations

Combining geometries via volumetric boolean operations amounts to simple mathematical operations

  • minimum or maximum function corresponds to intersection and union (respectively or reverse respectively deepening if inside is positive
  • multiplicative negation (commonly known as multiplication with minus one) turns a volumes inside out and vice versa – with that and the above one can construct differences

The issues with triangle meshes (piecewise linear B-Rep) in boolean operations

With triangulated surface meshes boolean operations are much more difficult.
Involving intersecting surface descriptions like triangle meshes, treatment of degenerate edge cases, and possible local re-meshing.

In the open source 3D modelling program blender that is being more aimed at visually pleasing results than good watertight meshes for manufacturing.
Using automatic booleans on triangle meshes is generally advised against (in favor of high effort manual tinkering) as it screws up the texture mapping.
All that manual tinkering on already triangulated meshed gets lost though when intersection and such need to be changed.
This is going strongly against reversible non-destructive modeling.

Coordinate transformations

  • linear transformations (translation, rotation, shear, mirror, boost) ...
  • nonlinear transformations (waves, swirls, twists, ...)

How it all goes together

(wiki-TODO: Explain this in more detail.)

The order of composition in the programmatic 3D modelling process differs from the order the math is finally evaluated.
E.g. a translation of a complex geometry at the end gets "threaded through" and is the first thing applied to the coordinates.

There are some neat tricks to do part of this on the type level.
Using type constructors X Y Z as placeholders for the coordinate axis values x y z.
This trick has been done in an F-Rep CSG library Implicitcad
(A domain specific 3D modelling library implemented in the programming language haskell)
In this particular example:

  • A lot of hard to trace indirection (somewhat typical for haskell) can make this quite hard to understand
  • In the case of haskell type level computing is kind of added as an after-though => consequence: incomprehensible error messages
  • Haskell is not a dependently typed language. So it has a value-level type-level barrier. This somehow feels like a big problem ...


(wiki-TODO: This seems important – discuss this ...)

  • First there is the domain specific modelling library code describing the geometry.
  • Then there is the single value of the entire 3D geometry with all the type constructors inside.

This eventually needs to go to:

Compiling exactly the same code to very different targets is the topic of: Compiling to categories (Conal Elliott).
So this might be highly relevant here. Deeper analysis needed.

F-Rep to polygonal B-Rep

In the course of the compilation to some target (being it for visualization or production)
at some point a conversion of F-Rep to something lower level becomes necessary.
This lower level intermediate compilation target (at least today in the case of FFF 3D printers) is usually B-rep.

  • It is in principle possible to jump to an even lower representation right away (for FFF 3D-printers that would be g-code)
  • It may also be possible to compile to something higher level like quadruplication (if that works).

In any case, for a compilation to a lower level some sort of discretization need to take place.
Points on the surface needs to be found with some root finding algorithm.

One interesting algorithm for triangulation may by like the following:

  • put a (to some degree triangulated) sphere inside the implicitly defined volume to triangulate
  • ray project the vertices out to the surface of the object
  • simulate mutual repulsion between the vertices under the constraint of staying on the surface till "reasonably" equilibrated
  • further subdivide the mesh
  • project the new points to the surface again
  • equilibrate again
  • repeat – edges and corners may need special attention in this algorithm.

Needed for root finding and this algorithm are not just

  • the implicit scalar function defining the volume but also
  • the first and likely second derivative.
  • The fist derivative of a scalar field is called "gradient" (tensor of rank one)
  • The second derivative of a scalar field is called "Hesse matrix" (tensor of rank two) – (Gaussian surface curvature is in there)

These are the first elements of a Taylor series that is approximating the surface locally.

An acceptably good way to do (such here needed) derivatives on computers is automatic differentiation.
Numerically implementing the definition of the limit is really ugly and bad software design.

An extremely elegant way to do automatic differentiation was presented in Beautiful differentiation (Conal Elliott). This:

  • Generalized to arbitrary dimension not just 3D but also 2D, 4D, and whatever-D
  • Generalized to arbitrary degree (as needed for a Taylor series)
  • Implements this employing lazy evaluation handling infinite partially unevaluated lists – this gives reasonably readable code

F-Rep challenges

Term simplification with a CAS

When big numbers of base geometries are combined this can lead to a really big symbolic expression.
The whole 3D models geometry is represented as one single formula (no matter how big).
One might need to simplify these in one way or another to get to acceptable performance.
Unfortunately this requires a full on computer algebra system (CAS) something that is typically not present as library in todays programming languages

  • The experiment in implementing "F-Rep CSG" in the sage computer algebra system ran into this problem:
    See: miniSageCAD
  • Interestingly Christian Scahfmeisters work on spiroligomers turned up similar algebraic simplification challenges

Term pruning

With max and min some parts of of the formula can completely cancel out for the most part of the total volume that the model occupies.
Thus there should also be other ways to prune out parts of the expression to avoid their unnecessary evaluation (and remember these pruneouts).

  • Binary space partitioning trees
  • Octrees
  • ...

Quadrics

Nice projections

Quadrics are a limited subset of algebraic varieties with some useful properties.
One of them is that projecting them to a lower dimension like 2D always yields nice formulas (2D quadrics).

Quadriculation

Quatrics may be usable for some non-trianle-based B-Rep. That is:
Maybe some king of "quarticulation" is possible, analogous to "triangulation" but adding continuity of the first derivative as additional boundary condition.

Related

  • Atomic orbitals – the implicit formulas can be used for F-Rep surface evaluation
    Note that these are single electron solutions. There are no exact solutions for multi electron atoms.
    The charge of the nucleus that is seen by an electron is gradually shielded towards the nucleus due to the other electron(s).

External links

Math

Data-structures fast lookup of stuff in 3D space:

Retrieved from "http://apm.bplaced.net/w/index.php?title=Constructive_solid_geometry&oldid=15249"