Difference between revisions of "Lattice scaled stiffness"

Revision as of 15:49, 1 June 2023

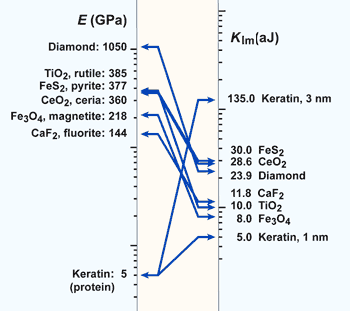
Young’s modulus and the lattice-scaled stiffness for selected materials – Modulus and lattice geometry data from multiple sources. Klm values for “keratin” represent building blocks of protein (or other folded polymers) with a keratin-like Young’s modulus, showing the effect of differing block sizes. (Description text as-is from Eric Drexlers blog)

In force applying mechanosynthesis
(when assuming one synthesizes the same material that the tool-tip is made out of)
the critical material property to look at is lattice scaled stiffness not just plain stiffness.

A bigger amplitude of thermal vibrations of a tool-tip in positional assembly is not critical
as long as the space between the spots where the block snaps to during deposition is is just big enough.
As long as the lattice spacing is big enough.

Math

[math] K_{lm} = E a^3 r^2_{err} [/math]

• E … Young’s modulus
• a … lattice parameter (a simplification, not all crystals have cubic symmetry)
• [math] r^2_{err} [/math] accounts for the ratio of the minimum error displacement to the lattice parameter
• [math] r_{err} = (1/2)^{1/2} [/math] is a common value.

Taken from Eric's Blog, See links below.

Related

• For now please consult the external links at the bottom pf the page: "Stiffness".
• A gemstone-like compound that supposedly has an especially good lattice scaled stiffness is ceria.
• Effective concentration – Lattice scaled stiffness boosts effective concentration where it's needed and depletes it where is is undesired.
• Piezochemical mechanosynthesis

• Tooltip cycle

External links

From Eric Drexler's blog partially dug up from the Internet Archive:

• 2009-02-15 Nanostructures, Nanomaterials, and Lattice-Scaled Stiffness
• 2009-02-10 Nanomachines, Nanomaterials, and K_lm