Difference between revisions of "Superlubricity"
From apm
(→Related: seperated off and made bold the link to superelasticity - highlighting unrelatedness and interestingness) |
(removed image of 3d printed modes - in now on page Atomically precise slide bearing which is now linked to) |
||
| (26 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
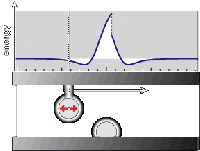
| − | [[File: | + | [[File:0315bearingSums.gif|thumb|400px|Graphic by Eric K. Drexler -- Citation: "Symmetric molecular bearings can exhibit low energy barriers that are insensitive to details of the potential energy function" <ref name="pdrag"> '''Drag mechanisms in symmetrical sleeve bearings:''' Drexler, K. E. (1992) ''[[Nanosystems]]: Molecular Machinery, Manufacturing, and Computation.'' Wiley/Interscience, pp.290–293.</ref>]] |
| − | [[File:Strained-shell-sleeve-bearing.gif|300px|thumb|right|A simulation made with the software "Nanoengineer-1" <br> Author Eric K. Drexler]] | + | [[File:Strained-shell-sleeve-bearing.gif|300px|thumb|right|A simulation made with the software "Nanoengineer-1" <br> Author Eric K. Drexler – An '''[[atomically precise slide bearing]]'''.]] |
| − | + | [[File:Nanotube-based-thermal-nanomotor1.jpg|400px|thumb|right|Coaxial nanotube bearing based nano-motors have been experimentally built and tested. While still very crude they already show very little friction. Much unlike the problems with [[stiction]] and wear in photolithographically produced [[MEMS systems]]. – Coaxial nanotubes are quite similar in characteristics to [[crystolecule]] bearing so the working nanotube bearings give '''experimental evidence for [[crystolecular element]]s working with low friction an [[wear free]]'''.]] | |
Up: [[Friction in gem-gum technology]] | Up: [[Friction in gem-gum technology]] | ||
| − | '''Superlubricity''' (or '''superlubrication''') is a '''state of extremely low friction''' that occurs when '''two atomically precise surfaces slide along each other''' in such a way that the '''"atomic bumps" do not mesh''' | + | '''Superlubricity''' (or '''superlubrication''') is a '''state of extremely low friction''' that occurs when '''two atomically precise surfaces slide along each other''' in such a way that the '''"atomic bumps" do not mesh'''. <br> |
| + | More precisely: When the lattices distances projected in the direction of movement are maximally incommensurate. | ||
| − | + | == Key aspects of superlubricity == | |
| − | + | ||
| − | + | * '''Present in [[gem-gum-tec]]:''' Superlubricity is present in [[crystolecule]] bearings which are essential [[molecular machine element]]s in [[gemstone metamaterial technology]]. | |
| + | * '''Eternally wear fee:''' Superlubricity features no "collinding mountainranges" at the nanoscale that can mutually shear off their tips. Thus superlubricating bearings are fully '''[[the ultimate construction toy|wear free]]'''. The dominating damage mechanism of superlubricating bearings is [[radiation damage|ionizing radiation]] or thermal destruction in extreme conditions (melting, evaporationg, hot chemical dissolution, ..). There is damage over time but there is no wear from mechanical friction (and load) over time. | ||
| + | |||
| + | == Examples exhibiting superlubricity == | ||
| − | |||
* two coplanar sheets of graphene rotated to one another to minimally mesh | * two coplanar sheets of graphene rotated to one another to minimally mesh | ||
| − | * two appropriately chosen tightly fitting coaxial nanotubes (experimantally demonstrated) {{wikitodo|add reference}} | + | * two appropriately chosen tightly fitting coaxial nanotubes (experimantally demonstrated) <br>{{wikitodo|add reference}} |
* [[diamondoid]] molecular bearings and other [[diamondoid molecular elements|DMEs]] with sliding interfaces. | * [[diamondoid]] molecular bearings and other [[diamondoid molecular elements|DMEs]] with sliding interfaces. | ||
| − | * an advanced [[metamaterial]] forming an [[infinitesimal bearing]] structure. | + | * an advanced [[metamaterial]] forming an [[infinitesimal bearing]] structure. |
| + | |||
| + | == Low friction without superlubricity == | ||
| + | |||
| + | There are a few notes about that on the page: "[[How friction diminishes at the nanoscale]]" | ||
| + | |||
| + | As long as the energy is efficiently recuperated when crossing repulsive angular locations <br> | ||
| + | Even bearings with large waviness of potential can have low friction. <br> | ||
| + | What absolutely must not happen is interfaces having such low stiffness that [[snapback]] is starting to occur. | ||
| + | |||
| + | == What kind of friction are we even talking about here? == | ||
| + | |||
| + | A very good question. <br> | ||
| + | |||
| + | === Classical static Friction? === | ||
| + | |||
| + | Well as soon as the waviness of the potential gets close and falls below | ||
| + | to the thermal energy (equipartitioning theorem) | ||
| + | there should be literally zero static friction. | ||
| + | There must be a point where a constant torque does not lead to a boundless acceleration. Hmm ... | ||
| + | |||
| + | But superlubricity is supposed to not have a point where it (more or less suddenly) falls to unmeasurably small levels like superconductivity. Hmm ... | ||
| + | |||
| + | === Friction from dynamic drag? === | ||
| + | |||
| + | Friction losses from dynamic (speed dependent) drag can get quite high. <br> | ||
| + | So drawing an analogy to superconduction here is far fetched. <br> | ||
| + | See numbers on the page: [[Friction in gem-gum technology]] | ||
| + | |||
| + | '''Band-stiffness scattering drag''' (BSSD) can be reduced by tuning for superlubrication: <br> | ||
| + | Interestingly there are two parameters. Not just the incommensurability. | ||
| + | |||
| + | * The '''velocity ratio of the alignment bands''' goes in '''quadratically''' <br><math> R = v_{bands} / v = |k_1| / |k_2 - k_1|</math> – [[Nanosystems]] (7.22) | ||
| + | * The '''relative amplitude of variations in stiffness''' of the interface at different angles goes in '''linearly''' <br><math> \Delta k_a / k_a</math> {{wikitodo|add a sketch}} | ||
| + | |||
| + | <math>P_{BSSdrag} \propto (\Delta k_a / k_a) R^2</math> – [[Nanosystems]] (10.23, 10.24) | ||
| + | |||
| + | '''Shear-reflection drag''' (SRD) is not influenced by these parameters. <br> | ||
| + | It is the remnant friction that remains in a well designed bearing. | ||
| + | |||
| + | Oddly simulations of nanotube bearings (see math on page [[Friction in gem-gum technology]]) are quite a bit above the point of dominance of shear-reflection drag. And that despite this being a quite conservative (pessimistic) estimation for levels of drag. | ||
| + | |||
| + | {{todo|Resolve the many not unrelevant mysteries here. More reading and thinking needed.}} | ||
| + | |||
| + | == Superlubricity - vs - Superconductivity == | ||
| + | |||
| + | The name "superlubricity" points to some weak analogies to [[superconductivity]]: | ||
| + | * similar: It is also a state of low energy dissipation during the motion of elemental particles | ||
| + | * dissimilar: It has no sharp onset/cutoff point and friction does not fall to unmeasurably low levels | ||
| + | * dissimilar: It is present at all (non destructive) temperatures including ~300K room temperature | ||
| + | * Superlubrication is reached by decrease of degree of intermeshment while superconductivity is reached by decrease of temperature. | ||
| + | * There is not a sharp cutoff in friction when decreasing the degree of intermeshment like the cutoff in superconductivity when decreasing temperature. | ||
| + | |||
| + | = Thresholds? = | ||
| + | |||
| + | <center> | ||
| + | {| | ||
| + | |[[File:0315pairPot.gif|200px|right|thumb|smoothly sliding atoms <br>– graphic by Erik K. Drexler]] | ||
| + | |[[File:0322pairSnap.gif|200px|right|thumb|unsmoothly sliding atoms <br>– graphic by Erik K. Drexler]] | ||
| + | |}</center> | ||
| + | |||
| + | When it comes to dynamic speed dependent friction the waviness of the energy potential is actually not that important. <br> | ||
| + | As long as there is no [[snapback]] the energy needed to overcome the next angle of maximum energy can be recuperated. | ||
| + | |||
| + | Thee is no special threshold for superlubricity, but there are other special thresholds: | ||
| + | * The waviness of the energy over the turning angle is exactly equal to the thermal energy per degree of freedom <br>(this is temperature dependent, but a constant for 300K room temperature) | ||
| + | * The interface is at the threshold to [[snapback]] | ||
| + | |||
| + | == Thermal activation energy - vs - Angular energy waviness == | ||
If [[positional atomic precision|AP]] surfaces are designed or aligned to not mesh then the "perceived bumps" (the bumps that the surfaces perceive as a whole) become lower and their spacial frequency becomes higher (more bumps per length). | If [[positional atomic precision|AP]] surfaces are designed or aligned to not mesh then the "perceived bumps" (the bumps that the surfaces perceive as a whole) become lower and their spacial frequency becomes higher (more bumps per length). | ||
If the surface pressure isn't extremely high '''the characteristic thermal energy k<sub>B</sub>T can become a lot higher than the bumps energy barriers'''. | If the surface pressure isn't extremely high '''the characteristic thermal energy k<sub>B</sub>T can become a lot higher than the bumps energy barriers'''. | ||
| − | Thus the friction becomes so low that e.g. an unconstrained [[diamondoid molecular elements|DMME]] bearing can be activated thermally and may starts turning randomly in a [//en.wikipedia.org/wiki/Brownian_motion Brownian] fashion '''[to verify]'''. | + | Thus the (static) friction becomes so low that e.g. an unconstrained [[diamondoid molecular elements|DMME]] bearing can be activated thermally and may starts turning randomly in a [//en.wikipedia.org/wiki/Brownian_motion Brownian] fashion '''[to verify]'''. |
| + | |||
| + | == Choice of [[nanoscale passivation]] and [[snapback]] dissipation == | ||
Oxygen or sulfur with their two bonds in a plane parallel to the relative sliding direction are a good choice for [[surface termination]] of bearing interfaces since this configuration gives maximal stiffness in sliding direction. | Oxygen or sulfur with their two bonds in a plane parallel to the relative sliding direction are a good choice for [[surface termination]] of bearing interfaces since this configuration gives maximal stiffness in sliding direction. | ||
| Line 24: | Line 97: | ||
If the two bonds of the atoms are instead in a plane normal to the sliding direction the lower stiffness may lead to higher energy dissipation (friction). Singly bonded hydrogen fluorine or chlorine passivations have even lower stiffness, see: [http://e-drexler.com/p/04/02/0315pairSnap.html E. Drexlers's blog: snap back dissipation]. This can be deliberately used in [[dissipative elements]] (friction brakes). There's a critical point at which snapping back starts to occur ['''todo:''' simulation results needed]. | If the two bonds of the atoms are instead in a plane normal to the sliding direction the lower stiffness may lead to higher energy dissipation (friction). Singly bonded hydrogen fluorine or chlorine passivations have even lower stiffness, see: [http://e-drexler.com/p/04/02/0315pairSnap.html E. Drexlers's blog: snap back dissipation]. This can be deliberately used in [[dissipative elements]] (friction brakes). There's a critical point at which snapping back starts to occur ['''todo:''' simulation results needed]. | ||
| − | + | = Main power dissipation mechanisms = | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{{todo|Integrate infos from [[Nanosystems]] and the "evaluating friction ..." paper.}} | {{todo|Integrate infos from [[Nanosystems]] and the "evaluating friction ..." paper.}} | ||
| Line 34: | Line 103: | ||
Main article: [[Friction mechanisms]] | Main article: [[Friction mechanisms]] | ||
| − | + | = Superlubricating crystolecule machine elements = | |
| − | + | == Atomically precise gemstone bearings == | |
| − | Interestingly Van der Waals | + | Interestingly [[Van der Waals force]]s allow for stable designs in which the axle in [[diamondoid molecular elements|gemstome bearings]] is pulled outward in all directions instead of compressed inward. <br> |
| + | This allows for lower friction at the cost of less load bearing capacity. | ||
| − | + | Stretching terminology a bit this could be counted as one form of [[Levitation]]. | |
| − | Gears with straight, while reducing atomic bumps due to roughly shape complementary, do not smooth out atomic bumps beyond that. <br> | + | * Q: How much can friction be lowered by this strategy? |
| − | Helical gears in contrast can and do smooth out atomic bumps. Up to some point the longer the contact between gear teeth the better the smoothing. This is a motivation to not make gears at the absolute minimal size possible but a bit above that. | + | * Q: Might resonant vibrations start to occur at high operation speeds? |
| + | |||
| + | == Atomically precise gemstone gears == | ||
| + | |||
| + | Gears with straight rows of teeth, while reducing atomic bumps due to being roughly shape complementary, do not smooth out atomic bumps beyond that. <br> | ||
| + | Helical gears in contrast can smooth out and do smooth out atomic bumps. <br> | ||
| + | Up to some point the longer the contact between gear teeth the better the smoothing. <br> | ||
| + | This is a motivation to not make gears at the absolute minimal size possible but a bit above that. | ||
<small>As a side-note: Another reason for making gears a bit above the absolute minimal size is that stiffness of the intermeshing gear teeth interface can be matched to the stiffness of the axles (preventing flex wave reflections in higher frequency operations).</small> | <small>As a side-note: Another reason for making gears a bit above the absolute minimal size is that stiffness of the intermeshing gear teeth interface can be matched to the stiffness of the axles (preventing flex wave reflections in higher frequency operations).</small> | ||
| − | + | == Rods in sleeves == | |
Challenges: | Challenges: | ||
| Line 53: | Line 130: | ||
* Getting a fit of just the right tightness with a compact sleeve around a thin reciprocative rod may be more difficult than getting just the right fit with a big stator sleeve around a big diameter rotor. Bigger loops can be finer adjusted in a relative sense. | * Getting a fit of just the right tightness with a compact sleeve around a thin reciprocative rod may be more difficult than getting just the right fit with a big stator sleeve around a big diameter rotor. Bigger loops can be finer adjusted in a relative sense. | ||
| − | + | = Snapping into place = | |
As mentioned before there is always a slight remaining ripple in the position dependant potential energy of the bearing (in its potential energy surface - PES). | As mentioned before there is always a slight remaining ripple in the position dependant potential energy of the bearing (in its potential energy surface - PES). | ||
| Line 59: | Line 136: | ||
(If quantum zero point energy isn't too high?) | (If quantum zero point energy isn't too high?) | ||
| − | + | = Quantum effects in (rotative) gemstone nanomachinery = | |
Quantisation of angular momentum is usually not present except for very small free rotating elements at very low temperatures. | Quantisation of angular momentum is usually not present except for very small free rotating elements at very low temperatures. | ||
| Line 69: | Line 146: | ||
* [[Nanomechanics is barely mechanical quantummechanics]] | * [[Nanomechanics is barely mechanical quantummechanics]] | ||
| − | + | = Related = | |
* More [[friction]] due to [[rising surface area]]. | * More [[friction]] due to [[rising surface area]]. | ||
| Line 76: | Line 153: | ||
* Superlubrication goes perfectly together with [[infinitesimal bearing]]s, reducing friction even further. | * Superlubrication goes perfectly together with [[infinitesimal bearing]]s, reducing friction even further. | ||
* [[Negative pressure bearings]] | * [[Negative pressure bearings]] | ||
| + | * [[Levitation]] | ||
----- | ----- | ||
* '''[[Superelasticity]]''' ... another performance parameter that can be unusually elevated at the nanoscale | * '''[[Superelasticity]]''' ... another performance parameter that can be unusually elevated at the nanoscale | ||
| − | == External links | + | == Concrete examples == |
| + | |||
| + | In [[atomically precise bearings]] like: | ||
| + | * The whole raceway of [[atomically precise slide bearing]]s | ||
| + | * The flanks of bigger [[atomically precise roller gearbearing]]s | ||
| + | |||
| + | Some of the the moving [[examples of diamondoid molecular machine elements]] <br> | ||
| + | feature tuned incommensurability and thus superlubricity. | ||
| + | |||
| + | = External links = | ||
'''Related pages on E. Drexlers homepage (internet archive):''' | '''Related pages on E. Drexlers homepage (internet archive):''' | ||
| Line 93: | Line 180: | ||
---- | ---- | ||
* Wikipedia: [http://en.wikipedia.org/wiki/Superlubricity Superlubricity] | * Wikipedia: [http://en.wikipedia.org/wiki/Superlubricity Superlubricity] | ||
| + | * Wikipedia: [https://en.wikipedia.org/wiki/Carbon_nanotube_nanomotor Carbon nanotube nanomotor] | ||
* Experiments with nanotubes: [http://www.nanowerk.com/spotlight/spotid=33115.php Superlubricity on the macroscale] | * Experiments with nanotubes: [http://www.nanowerk.com/spotlight/spotid=33115.php Superlubricity on the macroscale] | ||
| + | |||
| + | = References = | ||
| + | |||
| + | <references/> | ||
[[Category: Technology level III]] | [[Category: Technology level III]] | ||
[[Category: Technology level III]] | [[Category: Technology level III]] | ||
Latest revision as of 09:07, 29 August 2022
Graphic by Eric K. Drexler -- Citation: "Symmetric molecular bearings can exhibit low energy barriers that are insensitive to details of the potential energy function" [1]
A simulation made with the software "Nanoengineer-1"
Author Eric K. Drexler – An atomically precise slide bearing.
Author Eric K. Drexler – An atomically precise slide bearing.
Coaxial nanotube bearing based nano-motors have been experimentally built and tested. While still very crude they already show very little friction. Much unlike the problems with stiction and wear in photolithographically produced MEMS systems. – Coaxial nanotubes are quite similar in characteristics to crystolecule bearing so the working nanotube bearings give experimental evidence for crystolecular elements working with low friction an wear free.
Up: Friction in gem-gum technology
Superlubricity (or superlubrication) is a state of extremely low friction that occurs when two atomically precise surfaces slide along each other in such a way that the "atomic bumps" do not mesh.
More precisely: When the lattices distances projected in the direction of movement are maximally incommensurate.
Contents
- 1 Key aspects of superlubricity
- 2 Examples exhibiting superlubricity
- 3 Low friction without superlubricity
- 4 What kind of friction are we even talking about here?
- 5 Superlubricity - vs - Superconductivity
- 6 Thresholds?
- 7 Main power dissipation mechanisms
- 8 Superlubricating crystolecule machine elements
- 9 Snapping into place
- 10 Quantum effects in (rotative) gemstone nanomachinery
- 11 Related
- 12 External links
- 13 References
Key aspects of superlubricity
- Present in gem-gum-tec: Superlubricity is present in crystolecule bearings which are essential molecular machine elements in gemstone metamaterial technology.
- Eternally wear fee: Superlubricity features no "collinding mountainranges" at the nanoscale that can mutually shear off their tips. Thus superlubricating bearings are fully wear free. The dominating damage mechanism of superlubricating bearings is ionizing radiation or thermal destruction in extreme conditions (melting, evaporationg, hot chemical dissolution, ..). There is damage over time but there is no wear from mechanical friction (and load) over time.
Examples exhibiting superlubricity
- two coplanar sheets of graphene rotated to one another to minimally mesh
- two appropriately chosen tightly fitting coaxial nanotubes (experimantally demonstrated)
(wiki-TODO: add reference) - diamondoid molecular bearings and other DMEs with sliding interfaces.
- an advanced metamaterial forming an infinitesimal bearing structure.
Low friction without superlubricity
There are a few notes about that on the page: "How friction diminishes at the nanoscale"
As long as the energy is efficiently recuperated when crossing repulsive angular locations
Even bearings with large waviness of potential can have low friction.
What absolutely must not happen is interfaces having such low stiffness that snapback is starting to occur.
What kind of friction are we even talking about here?
A very good question.
Classical static Friction?
Well as soon as the waviness of the potential gets close and falls below to the thermal energy (equipartitioning theorem) there should be literally zero static friction. There must be a point where a constant torque does not lead to a boundless acceleration. Hmm ...
But superlubricity is supposed to not have a point where it (more or less suddenly) falls to unmeasurably small levels like superconductivity. Hmm ...
Friction from dynamic drag?
Friction losses from dynamic (speed dependent) drag can get quite high.
So drawing an analogy to superconduction here is far fetched.
See numbers on the page: Friction in gem-gum technology
Band-stiffness scattering drag (BSSD) can be reduced by tuning for superlubrication:
Interestingly there are two parameters. Not just the incommensurability.
- The velocity ratio of the alignment bands goes in quadratically
[math] R = v_{bands} / v = |k_1| / |k_2 - k_1|[/math] – Nanosystems (7.22) - The relative amplitude of variations in stiffness of the interface at different angles goes in linearly
[math] \Delta k_a / k_a[/math] (wiki-TODO: add a sketch)
[math]P_{BSSdrag} \propto (\Delta k_a / k_a) R^2[/math] – Nanosystems (10.23, 10.24)
Shear-reflection drag (SRD) is not influenced by these parameters.
It is the remnant friction that remains in a well designed bearing.
Oddly simulations of nanotube bearings (see math on page Friction in gem-gum technology) are quite a bit above the point of dominance of shear-reflection drag. And that despite this being a quite conservative (pessimistic) estimation for levels of drag.
(TODO: Resolve the many not unrelevant mysteries here. More reading and thinking needed.)
Superlubricity - vs - Superconductivity
The name "superlubricity" points to some weak analogies to superconductivity:
- similar: It is also a state of low energy dissipation during the motion of elemental particles
- dissimilar: It has no sharp onset/cutoff point and friction does not fall to unmeasurably low levels
- dissimilar: It is present at all (non destructive) temperatures including ~300K room temperature
- Superlubrication is reached by decrease of degree of intermeshment while superconductivity is reached by decrease of temperature.
- There is not a sharp cutoff in friction when decreasing the degree of intermeshment like the cutoff in superconductivity when decreasing temperature.
Thresholds?
When it comes to dynamic speed dependent friction the waviness of the energy potential is actually not that important.
As long as there is no snapback the energy needed to overcome the next angle of maximum energy can be recuperated.
Thee is no special threshold for superlubricity, but there are other special thresholds:
- The waviness of the energy over the turning angle is exactly equal to the thermal energy per degree of freedom
(this is temperature dependent, but a constant for 300K room temperature) - The interface is at the threshold to snapback
Thermal activation energy - vs - Angular energy waviness
If AP surfaces are designed or aligned to not mesh then the "perceived bumps" (the bumps that the surfaces perceive as a whole) become lower and their spacial frequency becomes higher (more bumps per length). If the surface pressure isn't extremely high the characteristic thermal energy kBT can become a lot higher than the bumps energy barriers. Thus the (static) friction becomes so low that e.g. an unconstrained DMME bearing can be activated thermally and may starts turning randomly in a Brownian fashion [to verify].
Choice of nanoscale passivation and snapback dissipation
Oxygen or sulfur with their two bonds in a plane parallel to the relative sliding direction are a good choice for surface termination of bearing interfaces since this configuration gives maximal stiffness in sliding direction.
If the two bonds of the atoms are instead in a plane normal to the sliding direction the lower stiffness may lead to higher energy dissipation (friction). Singly bonded hydrogen fluorine or chlorine passivations have even lower stiffness, see: E. Drexlers's blog: snap back dissipation. This can be deliberately used in dissipative elements (friction brakes). There's a critical point at which snapping back starts to occur [todo: simulation results needed].
Main power dissipation mechanisms
(TODO: Integrate infos from Nanosystems and the "evaluating friction ..." paper.)
Main article: Friction mechanisms
Superlubricating crystolecule machine elements
Atomically precise gemstone bearings
Interestingly Van der Waals forces allow for stable designs in which the axle in gemstome bearings is pulled outward in all directions instead of compressed inward.
This allows for lower friction at the cost of less load bearing capacity.
Stretching terminology a bit this could be counted as one form of Levitation.
- Q: How much can friction be lowered by this strategy?
- Q: Might resonant vibrations start to occur at high operation speeds?
Atomically precise gemstone gears
Gears with straight rows of teeth, while reducing atomic bumps due to being roughly shape complementary, do not smooth out atomic bumps beyond that.
Helical gears in contrast can smooth out and do smooth out atomic bumps.
Up to some point the longer the contact between gear teeth the better the smoothing.
This is a motivation to not make gears at the absolute minimal size possible but a bit above that.
As a side-note: Another reason for making gears a bit above the absolute minimal size is that stiffness of the intermeshing gear teeth interface can be matched to the stiffness of the axles (preventing flex wave reflections in higher frequency operations).
Rods in sleeves
Challenges:
- Using the same material for rod and sleeve can lead to pretty much the same spacing and no good superlubrication.
- Getting a fit of just the right tightness with a compact sleeve around a thin reciprocative rod may be more difficult than getting just the right fit with a big stator sleeve around a big diameter rotor. Bigger loops can be finer adjusted in a relative sense.
Snapping into place
As mentioned before there is always a slight remaining ripple in the position dependant potential energy of the bearing (in its potential energy surface - PES). This energy corresponds to the (very low) temperature under which the bearing starts to snap into place. (If quantum zero point energy isn't too high?)
Quantum effects in (rotative) gemstone nanomachinery
Quantisation of angular momentum is usually not present except for very small free rotating elements at very low temperatures. Axels in nanomechanical systems are usually coupled to a bigger system making their moment of inertia rather big. Free rotations will often be suppressed which leaves only torsional vibrations as possible degree of freedom.
See:
Related
- More friction due to rising surface area.
- Less friction: How friction diminishes at the nanoscale.
- Gem-like molecular elements or for short on this wiki here: crystolecules
- Superlubrication goes perfectly together with infinitesimal bearings, reducing friction even further.
- Negative pressure bearings
- Levitation
- Superelasticity ... another performance parameter that can be unusually elevated at the nanoscale
Concrete examples
In atomically precise bearings like:
- The whole raceway of atomically precise slide bearings
- The flanks of bigger atomically precise roller gearbearings
Some of the the moving examples of diamondoid molecular machine elements
feature tuned incommensurability and thus superlubricity.
External links
Related pages on E. Drexlers homepage (internet archive):
- Phonon drag in sleeve bearings can be orders of magnitude smaller than viscous drag in liquids
- Symmetric molecular bearings can exhibit low energy barriers that are insensitive to details of the potential energy function
- Stiffly supported sliding atoms have a smooth interaction potential
- Softly supported sliding atoms can undergo abrupt transitions in energy -- Related page: Snapback
- Paper: "Evaluating the Friction of Rotary Joints in Molecular Machines" (2017-01-27)
arXiv:1701.08202 [cond-mat.soft]; ResearchGate; pubs.rsc.org; Google Scholar
This uses simpified results from the Fluctuation-dissipation_theorem (Wikipedia-link)
- Zyvex: A Proof About Molecular Bearings by Ralph C. Merkle -- 1993
- Wikipedia: Superlubricity
- Wikipedia: Carbon nanotube nanomotor
- Experiments with nanotubes: Superlubricity on the macroscale
References
- ↑ Drag mechanisms in symmetrical sleeve bearings: Drexler, K. E. (1992) Nanosystems: Molecular Machinery, Manufacturing, and Computation. Wiley/Interscience, pp.290–293.
