Difference between revisions of "Same absolute speeds for smaller machinery"
m (Apm moved page Same absolute speed across scales to Same absolute speeds for smaller machinery: much more approachable for the random passerby) |
(added illustrative graphic, same as on page Higher throughput of smaller machinery) |
||
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | [[File:ConvergentAssemblyThroughputScalingLaw-compressed.jpg|400px|thumb|right|In this screencap of an animation the base assumption is "[[same absolute speeds for smaller machinery]]" (leading to linearly higher frequency of smaller machinery) this is only good as a first crude approximation. In an actual system one will want to slow down at the smallest scales, thus this geometry does not correspond to an actually proposed system, at least not at the smallest scales. More infos to this grapic on the page: [[Higher throughput of smaller machinery]].]] | |
| − | + | '''Constancy as the natural scaling option for speed of operations of machinery''' | |
What are the motivating factors to keep speed of machinery motions constant across scales (as a first approximation)? | What are the motivating factors to keep speed of machinery motions constant across scales (as a first approximation)? | ||
| − | * Keeping relative scale deflections from machine motions constant across scales | + | * Keeping relative scale deflections from machine motions constant across scales (see: [[Same relative deflections across scales]]) |
* Keeping friction losses constant across scales | * Keeping friction losses constant across scales | ||
| − | As it turns out both imply constant speeds across scales. | + | As it turns out both imply constant speeds across scales. <br> |
| + | There's a caveat for the latter motivating some deviation from constancy. <br> | ||
| + | A "tiny" bit of intentional slowdown. ("Tiny" meaning less than linear.) | ||
| + | |||
| + | '''Potential trapdoor to comprehension:''' Here "absolute speeds" refers to motion in terms of m/s (using SI units) <br> | ||
| + | It does not refer to frequencies (in Hertz or 1/s). For frequencies see: [[Scale natural frequency]]. <br> | ||
| + | ⚠️ '''One may colloquially say "smaller machinery moves faster" but in that case one is actually referinng to operation frequencies!''' | ||
== Keeping relative scale deflections from machine motions constant across scales == | == Keeping relative scale deflections from machine motions constant across scales == | ||
| Line 18: | Line 24: | ||
While one might expect losses to go up due to <br> | While one might expect losses to go up due to <br> | ||
| − | '''the well known scaling law of [[twice the surface area of half the volume]]''' applied to bearing area | + | '''the well known scaling law of [[twice the surface area of half the volume]]''' applied to bearing area, <br> |
| − | + | there is also the compensating factor of <br> | |
'''the poorly known scaling law of [[Higher throughput of smaller machinery]]'''. | '''the poorly known scaling law of [[Higher throughput of smaller machinery]]'''. | ||
| Line 32: | Line 38: | ||
'''Alternate natural scaling options for speed of operations of machinery.''' | '''Alternate natural scaling options for speed of operations of machinery.''' | ||
| − | Since dynamic friction scales quadratically with speed ([[Hundredfold smaller frictionlosses | + | Since dynamic friction scales quadratically with speed ([[Hundredfold smaller frictionlosses from tenfold slowdown]]) and <br> |
| − | Productive | + | Productive nanomachinery takes up very little volume ([[Higher throughput of smaller machinery]]) <br> |
it is possible to cheat by trading decreased speeds for increased volume of nanomachinery. | it is possible to cheat by trading decreased speeds for increased volume of nanomachinery. | ||
See: | See: | ||
| Line 42: | Line 48: | ||
---- | ---- | ||
| − | Optimal bearing technologies across scales likely change. <br> | + | Also: Optimal bearing technologies across scales likely change. <br> |
This makes deviating a bit from constant speeds across scales desirable. <br> | This makes deviating a bit from constant speeds across scales desirable. <br> | ||
See: [[Mesoscale friction]] | See: [[Mesoscale friction]] | ||
| Line 66: | Line 72: | ||
Related: [[Intuitive feel]] | Related: [[Intuitive feel]] | ||
| − | = Related = | + | == Related == |
* [[Scale natural frequency]] | * [[Scale natural frequency]] | ||
| − | * [[ | + | ---- |
| + | * [[Scaling law]] | ||
| + | ---- | ||
| + | * '''[[Same relative deflections across scales]]''' | ||
| + | * '''[[Higher throughput of smaller machinery]]''' | ||
[[Category:Scaling law]] | [[Category:Scaling law]] | ||
Latest revision as of 11:27, 15 September 2024
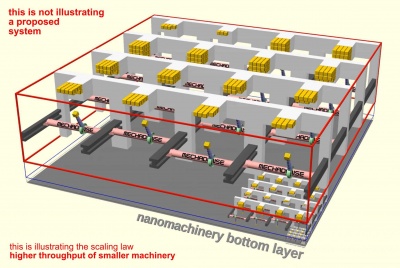
Constancy as the natural scaling option for speed of operations of machinery
What are the motivating factors to keep speed of machinery motions constant across scales (as a first approximation)?
- Keeping relative scale deflections from machine motions constant across scales (see: Same relative deflections across scales)
- Keeping friction losses constant across scales
As it turns out both imply constant speeds across scales.
There's a caveat for the latter motivating some deviation from constancy.
A "tiny" bit of intentional slowdown. ("Tiny" meaning less than linear.)
Potential trapdoor to comprehension: Here "absolute speeds" refers to motion in terms of m/s (using SI units)
It does not refer to frequencies (in Hertz or 1/s). For frequencies see: Scale natural frequency.
⚠️ One may colloquially say "smaller machinery moves faster" but in that case one is actually referinng to operation frequencies!
Contents
Keeping relative scale deflections from machine motions constant across scales
Keeping absolute speeds constant across scales
(or in other words keeping the same absolute speeds for smaller machinery)
can be considered as a natural choice when the main motivating factor is:
Same relative deflections across scales
Keeping friction losses constant across scales
While one might expect losses to go up due to
the well known scaling law of twice the surface area of half the volume applied to bearing area,
there is also the compensating factor of
the poorly known scaling law of Higher throughput of smaller machinery.
Both of these scaling laws are linear.
Thus for machinery of scale invariant throughput density and scale invariant operation speeds
they exactly compensate.
(wiki-TODO: Maybe bring this into a more formalized math form to make the point more clear.)
Important caveats – Leading to scaling of speeds that differ from constancy
Alternate natural scaling options for speed of operations of machinery.
Since dynamic friction scales quadratically with speed (Hundredfold smaller frictionlosses from tenfold slowdown) and
Productive nanomachinery takes up very little volume (Higher throughput of smaller machinery)
it is possible to cheat by trading decreased speeds for increased volume of nanomachinery.
See:
- Deliberate slowdown at the lower assembly levels
- Increasing bearing area to decrease friction
- Optimal sublayernumber for minimal friction
Also: Optimal bearing technologies across scales likely change.
This makes deviating a bit from constant speeds across scales desirable.
See: Mesoscale friction
Dispelling eventual concerns regarding convergent assembly
Adding convergent assembly levels atop that are exponentially growing in size
only adds at best logarithmic amounts of additional friction.
Thus it for the most part can be ignored.
Discussion of an perhaps counterintuitive aspect of constant speeds across scales
When conceptually for visualization scaling up just space but not scaling time,
then the assumption of constant speeds across scales leads to magnified models featuring magnified speeds.
One might intuitively expect increased wear and such, but this is misled.
High encounter frequencies are just natural at small scales (Scale natural frequency).
One should remember that even today's macroscale roller bearing in the end feature nanoscale surface-on-surface contacts.
The only change when going to bearings that as a hole are at the nanoscale is
that they necessarily need to be atomically precise because
the wear of imprecisions of the scale of today's macroscale bearings would annihilate nanoscale bearings instantly.
Or rather imprecisions of the scale of today's macroscale bearing can be bigger than whole nanoscale bearings.
Related: Intuitive feel