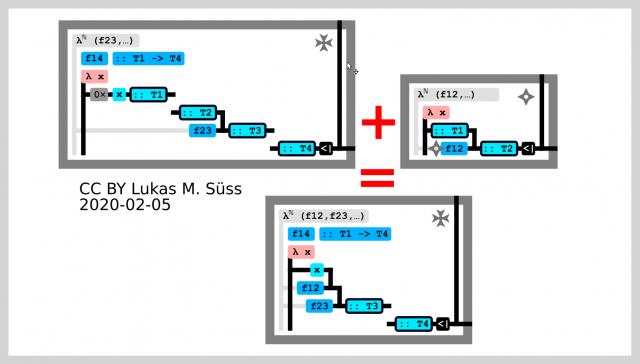
Annotated lambda diagram

Conversion of Cartesian coordinates to polar coordinates in the representation of annotated lambda diagrams.
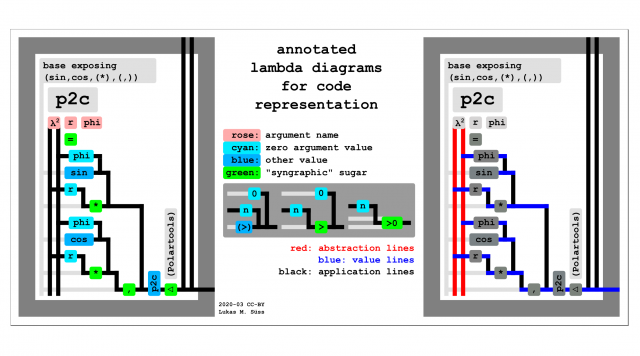
For details see: ALDs – example Cartesian to polar.

Quicksort algorithm as a single function in the representation of annotated lambda diagrams.
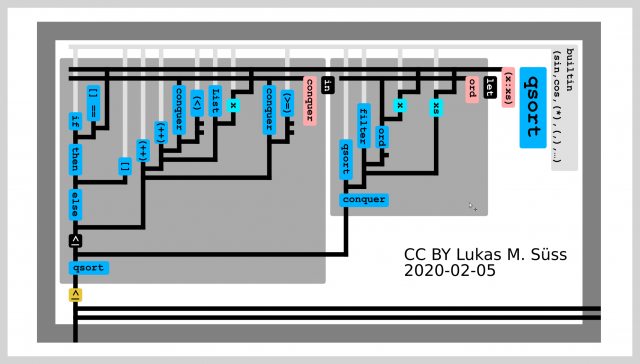
For details see: ALDs – example quicksort.

Introduction: The problem with current day programming

Current day (2021) programming has an accessibility problem.
The effect is that so called "end users" often see obvious trivial problems that they should be easily able to fix but can't because

• There is a stack of tools to learn before even to begin.
  – It's so bad that a job description emerged "full stack developer"
• Publishing something that is an interactive program is not easy anymore.
  – It's so bad that this bloated unnecessary process now has a name "deployment" a hole terminology and an "industry" around it has evolved
• The tools for programming either have a deterring learning curve or quickly run out of expressiveness.

The causes for this (on a highest abstraction-level) are likely twofold:

• (A) the increasing centralization of the internet – an emerging governance problem – (perhaps "eternally" periodically waving)
• (B) a technical software crisis – (sheer technical difficulty and an economics caused focus on short term investment focusing on symptoms rather than causes)

The Annotated lambda diagrams discussed here would be an attempt in tackling the latter point (B).

Lambda calculus – it's basic rules are unbelievably simple and it can compute anything and everything

Lambda diagrams are a way to visualize lambda calculus.
Lambda calculus is an extremely simple formalism that is equally expressive to the (much better known) Turing machine. That is: Lambda calculus is "Turing complete". Any program that is in principle logically possible can be written in Lambda calculus. A maximally universal computer. At least that is what is the current (2021) consensus on the topic.

The special thing about lambda calculus is that it is used very much unchanged as the core of a number of rather practical programming languages. Perhaps more so than the Truing machine is.

Graphical visualizations for lambda calculus

There are a number of graphical visualizations for Lambda calculus.
The most straightforward one is just to plot out the syntax tree.
There are only three elements in that syntax tree: abstractions, applications, and variables.

Plain lambda diagrams (PLDs)

An especially nice visualization for lambda calculus are (unannotated) "lambda diagrams".
These are presented by John Tromp on his homepage here: https://tromp.github.io/cl/diagrams.html

Annotated lambda diagrams (ALDs)

The basic idea in brief bullet points

• annotate plain lambda diagrams with: variable names, types, current values, kinds (aka types of types), ... (not all shown per default of course)
• Make them into a structured editor where you can type normally pretty much as you would in "plain textfile code editing"
  – (See: Fructure Specifically in this video with Andrew Blinn shortly after 6:03 [1] where he says "My preferred alternative is to simply type normally")
• Add progressive exposure!!!
• Make program fragments drag and drop interactive (like puzzle pieces)
  Give reasonable visual cues for efficiency (rather than fancy): identicons, arity mismatch visualization, ...
• Make them support typed holes of input, output, and bridge type.
  Such that program fragments are extendable: upstream, downstream, and ...
  can also be tied up in one or more still open concurrent paths (wiki-TODO: make a sketch)
• (Eventually make data flow around holes as far as this is possible. See: Hazel)
• Add type directed context sensitive suggestions for extending onto the present holes
• Put them into a zooming user interface (ZUI) that allows for (arbitrarily deep) in place evaluation preview
• Add inverse tabs – allowing to navigate the codebase different upstream paths that where formerly traced downstream
• Use an ultra finegrainedly content addressed programming language as a base!!!
  That in order to mop up with fragility of references, dependency hell and fix quite a number of other things too.
  (ony such language in construction as of 2021 seems to be the unison language)

---

Eventually add higher level data visualization:

• that follow code structure (see: Tangible values – by Conal Elliott) – but with added progressive exposure.
• that give an immediate connection by bidirectional data-flow (see: Drawing Dynamic Visualizations – by Bret Victor) (See: enso language)

Totally trearing down the GUI vs commandline rift!

The idea is as follows:
If all progressive exposure is closed then the UI is completely indistinguishable from a conventuinal GUI.
Except one little "+" or something as the starting point for progressive exposure.
A progressive exposure step opens up the ALD that corresponds to the visual element.
From there the "end-user" (now elevated to "deveuser") can trace the codebase to non-displayed or even non-visual code elements.
Trace via the the nicely visually traceable lines in the ALD.

Exposing enough GUI elements and hiding the visualization one eventually ends up with Just ALDs or
some other code projection like conventional purely textual ones.

Add to that: Bookmarking of "interface visualizations" and
organizing "code" documentation and data storage in a desktop wiki like system that
is implemented in that whole programming system in a bootstrapped way.

The basic benefits

Combines the best of the two worlds of textual and graphical code:

• Almost as traceable as graphical code (since there are traceable "program circuit" lines)
  – these lines are quite different to "conventional" graphical programming though
• Almost as scaleable as textual code (since the structure closely follows textual code) – a little less dense

Does NOT combine the worst of the two worlds:

• unscalability of graphical wire-monster-krakens and
• hard tracability of excessively indirected textual codebases)

---

• Seeing the whole code multiverse at a glance and and the live running state as a literal "red thread" within.
• Browsing the codebase in all dimensions without detours and disruptive jumps
  Human mental RAM is limited, it shouldn't be used for pointless navigation hurdles.

Mockup Demos

Note: If actually implemented all this should be dynamic and interactive

Drag and drop interaction with program fragments and typed holes

Moving program fragments through programs and linking them up via typed hole connection ports

Dragging the program fragment f12 (upper right) into an other yet incomplete function f14 where the types (T1 and T2) match up and connections snap in place. Only unsaturated type-holes display their type to keep visual noise low.

Dragging the function f12 (upper right) into an other yet incomplete function f14 where the types (T1 and T2) match up and connections snap in place. Imagine the whole thing interactive and animated. As soon as f12 is dragged into the box of f14 it'd get displayed in the same simplified way ad f23 already is. This is not shown. Dragging f12 around in the box of f14 will move stuff around to make space accordingly.
Wrong connections can be enforced this will make explicit typed holes of bridge type (bridge holes). Not shown.

• Grey cross upper right means this function is expanded and its definition is shown
• Grey shuriken like star upper right means this function is collapsed and its definition is hidden
• Note how f12 (once dropped into f14) gets added to the collected semi-implicit dependencies of f14 (light grey annootations)

Visual cues employing human image reconition skills – identicons and arity cues

Visual cues employing human image recognition capability. This might seem a bit playful and silly, but employed correctly this might give a notable increase in enjoyment and productivity when telling computers what to do. Note that only unsaturated holes (the construction sites of coding) would get displayed highly "visually verbosely" be default.

Mockups still TODO

• Continuous transformation from the abstract syntax tree (a s a most direct code projection) to ALDs as code projection
• Representation of "algrebraic effects (or abilities)" in ALDs (maybe not a nice match – unfortunately ...)
• Investigate representation of typeclasses in ALDs (typeclasses similar to what is present in the programming language haskell)

Mockups regarding Conal Elliotts work

Tangible values (TVs)

The desire:
Totally obliterating the GUI-vs-commandline rift by combining tangible-value-GUIs with a spectrum of code projections all the way to textual.
Annotated lambda diagrams sitting smack in the middle between graphical and textual.

Priority #1:

• Investigate Conal Elliots work about "tangible values" in the context of ALDs

Tangible values may give a GUI that is pretty much indistinguishable for the GUI's we have today.
But with all windows and graphical elements "secretly" being tangible values in the background.
Assuming the inverse operation of tangible-value-fusion (let's call it "fission" here) is implemented too (which absolutely must be done IMO)
then the tangible values (as GUI elements) already come with some progressive disclosure.

Progressive disclosure by "fission" can only expose things that do have already implemented graphical representations though.
So my idea here (beyond what Conal Elliott presented in his demo "Eros") is to allow for progressive disclosure of the code
that is associated with the tangible not just via fission but also via annotated lambda diagrams (and even textual code projections if so desired).
(Which come with their own mean of progressive disclosure that is ZUI zooming)
Any combination goes. (only TV, ALD+TV, only TV – having relative scaling adjustable should be useful e.g. by local scrolling)

Related notes:

• Default values (for looking at a slice of a stateless tangible value) are living outside the stateless realm.
  They can be stored on disk as additional necessarily stateful data.
  
• Code flowing around holes on the data level rather than the type level (See: Hazel) might be very useful.

Compiling to categories

Priority #2:

• Investigate Conal Elliots work "Compiling to Categories" (which is abstracting with closed cartesian categories CCCs over lambda calculus)
  But that done from within ALDs (which essentially are lambda calculus)
  Out of this reason this likely won't yield a nice representation. Maybe? Still interesting to investigate.

Beautiful differentiation

Priority #3:

• Investigate Conal Elliots work "Beautiful differentiation" – Will just turn into a library I guess

Mockups regarding maybe not so practical stuff

• Church encoding in lambda diagrams – more efficient binary encoding
• Encoding of list and enums (product types and sum types respectively) – there's a certain interesting asymmetry in minimal encoding (wiki-TODO: dig that out and link it here)
• What about progressive exposure all the way down to the bits and bytes of an open source processor with extensionally equivalent naive inefficient implementations both serving as documentation but still switchable in – Related: Multiplication circuits (and their surprising richness), Ternary logic, p-adic numnbers, ...

Warning! you are moving into more speculative areas.

• Relation of typed holes to the void type, absurd function and the like – "void" being sort of on the top of the infinite pecking order: type, kind (type of type), sort (type of type of type), ... not inside of any provably terminating "toy formalism"

Notes on conventional/classical "graphical programming" code projections

Conventional graphical programming typically follows the scheme of data-wires and function-boxes.
Thee are approaches that reverse that function-wires and data-boxes but that seems just bad in a different way.

Note: Assuming a function B (represented as a box) has an input that accept a function as an input (that is the function is a so called "higher order function")
then the wire transmitting some other input function to that input is still a "data wire"!
In contrast a function wire is a wire that represent a data-transformation itself.
(Most graphical programming tools do not even allow for using data wires as channels for transmission of functions.)

---

Annotated lambda diagrams (only a "semi graphical" code projection)
have inherently integrated the capability of overloading the meaning of the graphical lines that connect to other lines.
E.g. monoids, applicative functors, monads, ...
What may seem like boxes are just annotations of the lines.
That is removing the boxes the code still works.
That is not the case for classical graphical programming.

This can be done in classical box and wire representation too.
But it is not inherent. That is not something what one would implement in an naive approach.
And thus it is has rarely (never?) been done.
One concrete case of a programming language attempting that is the (multi representational) language called enso (formerly luna).

What is truly unique to ALDs -- the semi graphical code projection of ALDs is that
Abstractions and applications remain separate in the graphical representations.
(TODO: think about why this might be the killer advantage over box and wire representation)

External links

A basic write-up of some ideas with links to twitter posts.
(wiki-TODO: this needs to be published more properly (that is: more resilliently))

• (Forum: HC => Channel: Technical Watercooler => Topic: Future of Coding)

---

Zooming user interface:
For many user interfaces this idea seems rather impractical.
It is likely extremely useful for the case of ALD's though.