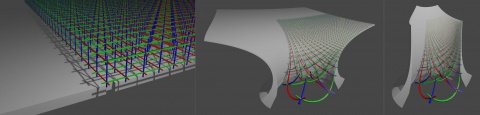
Log polar mapping

As this is logarithmic infinitely small scale is infinitely far down the z-direction. The inner yellow cylinders inner volume is mapped from the entire positive half-space. The outer blue cylinder rings volume is mapped from the entire negative half-space. As the latter is heavily distorted it's better to stick just to the former for visualizations. The positive z-axis remains on the z axis. That's perhaps the easiest to comprehend part. The xy-plane maps to the yellow cylinders wall. The negative z axis maps to the outermost blue cylinder wall. Outside that there is forbidden space not being mapped to from any real valued xyz-position. This forbidden space is safely ignorable. Scaleable vectrorgrapic version.

Illustrating log polar mapping by a morphing from non-transfromed coordinates. Note that for a morph a specific scale needs to be picked. Also note that the grey wall curls outward. That means it sits below the xy-plane in the negative half-space.

Here mapped is both a c coordinate grid and molecular mill rotors analog to the ones seen in: "Productive Nanosystems from Molecules to Superproducts". Note that in non-transformed coordinates the grey wall sits on xy-plane partly above partly below. Thus it gets curls both ways in the magnifying log polar coordinates. The wide bottom is a small cutout around (0,0,0) that's necessary as nearing zero everything gets exponentially magnified.

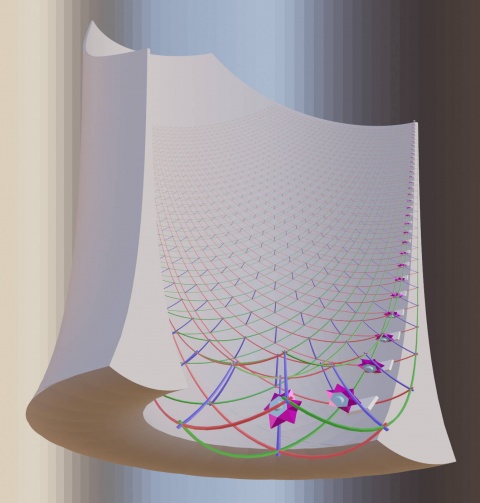
This page is about a generalization of log-polar mapping to 3D space. Specifically usable as one of the visualization methods for gemstone metamaterial factories and as one of the distorted visualization methods for convergent assembly.

Motivation

Log polar mapping should be well suitable for a static poster showing all relevant internals of a nanofactory.
Being able to display/visualize all the convergent assembly levels (and routing levels) of an entire nanofactory all at once (in 3D) without needing to resort to a animation/video format doing some zooming in/out. Displaying more at once also makes more apparent that smaller machinery operates at higher frequency (not higher speed though - careful!).

Animation can still be added showing the activity at all scales at once and making the continuity of matter transport more obvious. Logistics and things like level crossing lag to the first initial output.

Displaying many scales and their relation simultaneously

This can be done by generalizing log polar mapping to 3D like so:

• x'(x,y,z) = pi/2 - atan2( z, sqrt(pow(x,2) + pow(y,2)) ) * cos(atan2(y,x)))
• y'(x,y,z) = pi/2 - atan2( z, sqrt(pow(x,2) + pow(y,2)) ) * sin(atan2(y,x)))
• z'(x,y,z) = log( sqrt(pow(x,2) + pow(y,2) + pow(z,2)) ) / log(base)

This is a natural generalization of the much more commonly used 2D case.

Relation to more common 2D log polar mapping

Using z instead of y to better match the analogy.

• x' = atan2(y,x)
• z' = log( sqrt(pow(x,2) + pow(z,2)) ) / log(base)

In both 2D and 3D case: z' corresponds to the radius of a circle or sphere (respectively) just logarithmized.
This should be reasonably intuitive to comprehend.
The logarithm is converting scale invariance/symmetry into translational invariance/symmetry.

In the 2D case: x' corresponds to the the angle on a circle. Unrolling a circle. Quite intuitively to comprehend.
In the 3D case: x' and y' correspond going around a sphere in the direction given by the y/x ratio ~ atan2(y/x).

Unlike in the 2D case where one can go the full 360° without any issue,
in the 3D case after going 90° (and thus crossing the xy-plane) the sphere at a
constant cutting cylinder radius gets smaller again and eventually meets up
with coming around the sphere from other sides.

For that reason for the negative 3D half-space is being heavily distorted
(to the point that the 1D linear negative z-axis is blown up to a 2D cylinder wall).
Using just the positive half-space though is plenty for illustrating convergent assembly where there is a bottom.

Related

• Distorted visualization methods for convergent assembly
• Visualization methods for gemstone metamaterial factories
• Challenges in the visualization of gem-gum factories

External links

• https://en.wikipedia.org/wiki/Log-polar_coordinates
• 1996 – An Introduction to the Log-Polar Mapping – Helder J. AraujoJorge Miranda DiasJorge Miranda Dias – ResearchGate

Not log polar mapping but mercator projection to the extreme.
This should be locally similar to log polar mapping in that math in the limit becomes identical.
https://mrgris.com/projects/merc-extreme/