Annotated lambda diagram mockups

From apm
Revision as of 23:44, 22 September 2021 by Apm (Talk | contribs) (→‎Annotated lambda diagrams with zooming user interface as a window into the entire control flow multiverse: spelling)

Jump to: navigation, search

Annotated lambda diagrams (ALDs) are a proposed interactive programming interface.
This page presents some mockups about what functionalities could be implemented and how they could be used.
For a basic gist about ALDs see main page: Annotated lambda diagrams

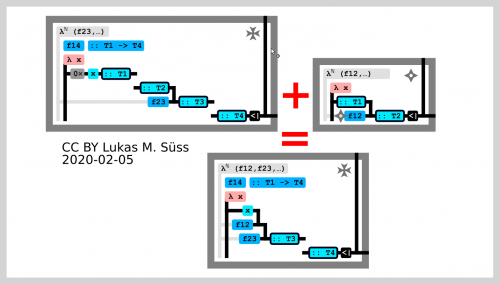
Drag and drop interaction with program fragments and typed holes

Moving program fragments through programs and linking them up via typed hole connection ports

Dragging the program fragment f12 (upper right) into an other yet incomplete function f14 where the types (T1 and T2) match up and connections snap in place. Only unsaturated type-holes display their type to keep visual noise low.

Dragging the function f12 (upper right) into an other yet incomplete function f14 where the types (T1 and T2) match up and connections snap in place. Imagine the whole thing interactive and animated. As soon as f12 is dragged into the box of f14 it'd get displayed in the same simplified way ad f23 already is. This is not shown. Dragging f12 around in the box of f14 will move stuff around to make space accordingly.
Wrong connections can be enforced this will make explicit typed holes of bridge type (bridge holes). Not shown.

  • Grey cross upper right means this function is expanded and its definition is shown
  • Grey shuriken like star upper right means this function is collapsed and its definition is hidden
  • Note how f12 (once dropped into f14) gets added to the collected semi-implicit dependencies of f14 (light grey annootations)

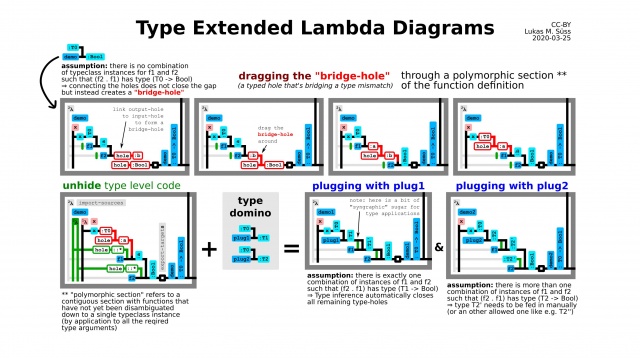
Dragging "bridge-holes" or "gap-holes" through still ambiguous sections of the code

Dragging "bridge holes" through sections of code that are still ambiguous in type. That would be an interesting exotic feature to have. It's kind of complementary to dragging functions or program fragments around.

Visual cues employing human image reconition skills – identicons and arity cues

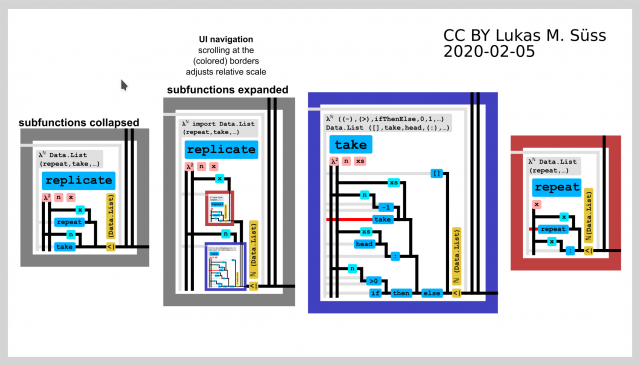
Visual cues employing human image recognition capability. This might seem a bit playful and silly, but employed correctly this might give a notable increase in enjoyment and productivity when telling computers what to do. Note that only unsaturated holes (the construction sites of coding) would get displayed highly "visually verbosely" be default.

Zooming user interface (ZUI)

From scaled down in place preview to zooming user interface

In place code preview in annotated lambda diagrams

This mockup was put together in order to illustrate how annotated lambda diagrams would allow for
an (adjustably) scaled-down in-place preview of functions on which the currently looked at function depends on.

Specifically this random example code (the "replicate"-function) takes a value and a natural number and
returns a list of copies of that value with the length of that natural number.

In place preview:
Check out the "replicate"-function (grey border).
Looking closely into the expanded version (second from left) you can see:

  • the scaled down "in place preview" of the "take"-function (blue border) and
  • the scaled down "in place preview" of the "repeat"-function (red border)

This is not yet an evaluating substitution!
Note that (despite this looking like a substitution) this is only just a yet-unevaluated in-place-preview.
This is important. This is very different to "conventional" box and wire graphical programming.
(matching the structure of the plain lambda diagrams)

Actual honest-to-goodness evaluation amounts to short-circuiting:

  • vertical-abstraction-lines (always on the right) with
  • vertical application-lines (always on the left).

That entails:

  • all abstraction lines of the substituted in function that got saturated just vanish (note that partial application is allowed)
  • what was formally supplied via the lines now gone is now supplied by the abstraction lines of the callee
  • former guts of the now substituted-in function are now arbitrarily complexly intertwined into the calling function

Note that with true substituting evaluation there is a loss decomposition.
Creating complex patterns from simple rules is the point of programming after all.

Is this true?: Classical box-and-wire graphical programming cannot make a distinction between in-place-preview and actual substitution?
If so we might be onto something here.

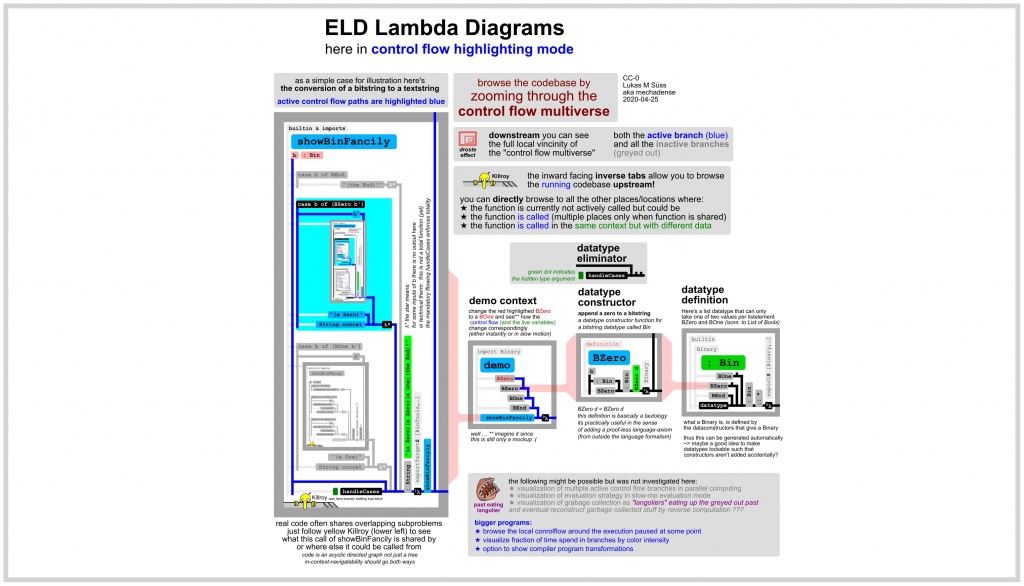
Annotated lambda diagrams with zooming user interface as a window into the entire control flow multiverse

The desire here is to implement in place previews (with adjustable relative scaling factor)
to annotated lambda diagrams in such a way that:

  • in place previews can be arbitrarily deeply nested.
  • one can zoom-travel though all of this via a global zoom going across all nesting levels (at least global in a viewport window)

The representation would allow for visualization of the activity of the garbare collector.

Peering into the entirety of the control flow multiverse while it's running live. The lines highlighted in dark blue mark the control flow path that is active at the current moment of execution time (possibly paused). A bright cyan background marks the active case-of-branches. – The "demo" function performs constructive corecursion with dataconstructors. The "showBinFancily" function performs deconstructive recursion with the case of construct. (TODO: Investigate avoiding recursive definitions alltogether. See Book: "The Little Typer")

Some of the massive practical challenges in implementing an ALD-ZUI:
Typical graphic GUI libraries are totally

  • not built for zooming user interface (ZUI) like zoomability and
  • not built for displaying very very big numbers of elements.

Even with special purpose solutions it is difficult ...

A naive redraw of the whole screen for every frame (as often done in computer games)
is is not a viable option (for anything beyond an interactive mockup prototype).
Instead usage of off-screen graphic buffers is essential – partially updated not fully redrawn
(this is e.g. not supported by the webgl wrapper-libraries of the elm language as of 2021 – learned the hard way).
Redrawing only the changing graphic details on mutable graphics-buffers
can easily lead to graphic glitch like artifacts from bugs if not done
with proper fool-proof usually performance expensive abstractions.
Further adding to the difficulty here.

The design choice for off-screen partially updated graphic-buffers becomes necessary due to the following challenges and requirements:

  • With tree like visual nesting the amount of elements displayed on screen can grow very fast to seriously problematic numbers.
  • In a live coding mode (that should be supported) a lot of the displayed elements may need to be refreshed at a high frame rate.
  • As soon as the computer idles the CPU/GPU load should drop to near zero because this is not a computer game where permanent high load is acceptable.

Furthermore:
Regular rescaling of the zoom level during intense zoom-navigation is essential. This is:

  • to prevent very quickly running out of the number-range that float-values can represent without rounding errors
  • to make dropping off (or heuristic pre-loading) of parts of the visualization easier that are way too small or way too big to see.

Notice the interesting duality of:

  • the type-constructors used to construct a value in the "demo" function – constructive corecursion
  • the case-of type-destructors used to destruct that value in the "showBinFancily" function – destructive recursion – handleCases

Maybe interesting side-note: There is definition by (not necessarily terminating) recursion present here.
There are ways to avoid "definition by recursion" alltogether.
All that is needed is a termination case and a provable overall monotonous approach towards that termination case. Well, these can be obfuscating and brain bending.
This is related to:

"Inverse tabs" for browsing the whole codebase graph rather than only the local code dependency tree

The obvious code navigation options include:

  • Tracing down to the codebase into the dependencies (the functions that the currently observed function depends on) and going back up that same path again.
  • Following the codebase along the some execution trace.

This is not enough!!
We need "inverse tabs".
We want also be able to quickly jump to functions that answer the question:
What other functions do call this function too that we currently look at?
By switching over to a different "inverse tab" one keeps looking at the same function in the tab but
the whole surrounding (visually represented) context gets switched out.
So when zooming out by scrolling one goes a different way in the codebase.

Essentially this gives one access to the whole directed graph of the codebase not just to a local dependency tree.

Inverse tabs are indicated in the mockup graphic about "peering into the control flow multiverse" at the lower left.
To make it easier to reference to a yellow killroy face has been added.
(wiki-TODO: Make a new mockup focused on showing the idea of inverse tans better.)

Mockups regarding Conal Elliotts work

Tangible values (TVs)

The desire:
Totally obliterating the GUI-vs-commandline rift by combining tangible-value-GUIs with a spectrum of code projections all the way to textual.
Annotated lambda diagrams sitting smack in the middle between graphical and textual.

Priority #1:

  • Investigate Conal Elliots work about "tangible values" in the context of ALDs

Tangible values may give a GUI that is pretty much indistinguishable for the GUI's we have today.
But with all windows and graphical elements "secretly" being tangible values in the background.
Assuming the inverse operation of tangible-value-fusion (let's call it "fission" here) is implemented too (which absolutely must be done IMO)
then the tangible values (as GUI elements) already come with some progressive disclosure.

Progressive disclosure by "fission" can only expose things that do have already implemented graphical representations though.
So my idea here (beyond what Conal Elliott presented in his demo "Eros") is to allow for progressive disclosure of the code
that is associated with the tangible not just via fission but also via annotated lambda diagrams (and even textual code projections if so desired).
(Which come with their own mean of progressive disclosure that is ZUI zooming)
Any combination goes. (only TV, ALD+TV, only TV – having relative scaling adjustable should be useful e.g. by local scrolling)

Related notes:

  • Default values (for looking at a slice of a stateless tangible value) are living outside the stateless realm.
    They can be stored on disk as additional necessarily stateful data.
  • Code flowing around holes on the data level rather than the type level (See: Hazel) might be very useful.

Compiling to categories

Priority #2:

  • Investigate Conal Elliots work "Compiling to Categories" (which is abstracting with closed cartesian categories CCCs over lambda calculus)
    But that done from within ALDs (which essentially are lambda calculus)
    Out of this reason this likely won't yield a nice representation. Maybe? Still interesting to investigate.

Beautiful differentiation

Priority #3:

  • Investigate Conal Elliots work "Beautiful differentiation" – Will just turn into a library I guess

Overloading the meaning of the lines – (applicative funtors, monads, ...)

(wiki-TODO: add the mockup showing a monad in lambda diagrams)

Mockups still TODO

  • Continuous transformation from the abstract syntax tree (a s a most direct code projection) to ALDs as code projection
  • Representation of "algrebraic effects (or abilities)" in ALDs (maybe not a nice match – unfortunately ...)
  • Investigate representation of typeclasses in ALDs (typeclasses similar to what is present in the programming language haskell)

Investigate porting some of Jonathan Edwards work in his subtext demo series to ALDs: ( https://vimeo.com/jonathoda )

  • No Ifs, Ands, or Buts 2016 – Uncovering the Simplicity of Conditionals – Jonathan Edwards
    – MIT Computer Science and Artificial Intelligence Lab
    – (pdf) – (video)
  • Reifying programming 2017
  • Direct Programming 2018

Mockups regarding maybe not so practical stuff

  • Church encoding in lambda diagrams – more efficient binary encoding
  • Encoding of list and enums (product types and sum types respectively) – there's a certain interesting asymmetry in minimal encoding
    (wiki-TODO: dig that out and link it here)
  • What about progressive exposure all the way down to the bits and bytes of an open source processor with extensionally equivalent naive inefficient implementations both serving as documentation but still switchable in – Related: Multiplication circuits (and their surprising richness), Ternary logic, p-adic numnbers, ...

Warning! you are moving into more speculative areas.

  • Relation of typed holes to the void type, absurd function and the like – "void" being sort of on the top of the infinite pecking order: type, kind (type of type), sort (type of type of type), ... not inside of any provably terminating "toy formalism"

Notes on conventional/classical "graphical programming" code projections

Conventional graphical programming typically follows the scheme of data-wires and function-boxes.
Thee are approaches that reverse that function-wires and data-boxes but that seems just bad in a different way.

Note: Assuming a function B (represented as a box) has an input that accept a function as an input (that is the function is a so called "higher order function")
then the wire transmitting some other input function to that input is still a "data wire"!
In contrast a function wire is a wire that represent a data-transformation itself.
(Most graphical programming tools do not even allow for using data wires as channels for transmission of functions.)

Annotated lambda diagrams (only a "semi graphical" code projection)
have inherently integrated the capability of overloading the meaning of the graphical lines that connect to other lines.
E.g. monoids, applicative functors, monads, ...
What may seem like boxes are just annotations of the lines.
That is removing the boxes the code still works.
That is not the case for classical graphical programming.

This can be done in classical box and wire representation too.
But it is not inherent. That is not something what one would implement in an naive approach.
And thus it is has rarely (never?) been done.
One concrete case of a programming language attempting that is the (multi representational) language called enso (formerly luna).

What is truly unique to ALDs -- the semi graphical code projection of ALDs is that
Abstractions and applications remain separate in the graphical representations.
(TODO: think about why this might be the killer advantage over box and wire representation)

Related

Retrieved from "http://apm.bplaced.net/w/index.php?title=Annotated_lambda_diagram_mockups&oldid=12040"