Difference between revisions of "Reversible computation"

Revision as of 12:07, 2 September 2024

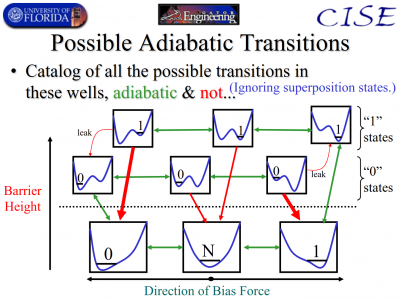
This is how one switches a bit from 0 to 1 or vice-versa losslessly and thus the basis of reversible computing. Red arrows are lossy/dissipative/irreversible well merging processes. Follow the spiral of green arrows to go from a 0 to a 1 (or vice versa) in a lossless/nondissipative/reversible/adiabatic manner.

The extremely simple but too naive approach

Any logic gate can be naively made into a reversible one by just not throwing away the inputs.
That strategy is obviously using up an ever growing and impractically large amount of data storage space though.
To avoid running out of memory (to keep space complexity low) the approach must be changed.

Logic gates and circuitry can be optimized (Toffoli gate ...) but this alone does not change much.
Space usage is still monotonously growing with computation steps taken.

Retractile cascades and reversible computation trees

Te main way to get space back is to store the (intermediate) results of a computation and then "uncompute" the path to the the result.
The "uncomputation" recuperates the Helmholtz free energy associated with the bits of information that needed to be temporarily stored during the computation.
This computation then storing then uncomputation is called a "retractile cascade".

Tightly nesting retractile cascaded leads to a reversible computation tree.
There are several strategies to optimize both space and time efficiency.

To get an intuitive understanding of how the energy recuperation in "retractile cascades" and reversibly computation trees work
looking at a minimal demonstration problem implemented in mechanical reciprocative rod logic might help.

Limits to spacetime efficiency for reversible computation

Strongly simplified (take it with a grain of salt):
It seems reversible computation can (for the completely general case!) never by as spacetime efficient as irreversible computation.
If the same efficiency were possible then ALL asymmetric difficulty problems (a foundation of current day 2021 cryptography) would be cracked
by implementing the easy forward problems as efficient as in irreversible computation and then "simply" running them backward with the exact same spacetime complexity.

This would not just break prime factorization (like quantum computation does) but all asymmetric difficulty problems.

Avoiding the limit of spacetime efficiency for reversible computation

For many special case classes of computation (that is classes for many classes of programs) though
the the same spacetime efficiency as with irreversible computation IS possible.

The main benefit of of sticking to full on true reversible computation is extremely low power consumption.

Relation of reversible computation to purely functional programming

purely functional programming is a weaker requirement than reversible computation though since:

• it only calls for extensional logic reversibility (same input always leads to same output)
• it does not call for intensional energetic/entropic reversibility (destructive overwrites of data inside are allowed as long as they are (provably!) kept encapsulated.
  That is: Any amount of Helmholtz free energy may be irreversibly devaluated.
  There can be a destructively overwriting state changing "UnsafePerformXY" method buried
  down somewhere in the depths of a function that is extensionally a safe purely functional function.

Through that weaker requirement of only higher level logical reversibility:

• one looses the property of low power consumption.
• one (probably) lifts the fundamental limit of being fundamentally weaker than irreversible programming (here imperative programming)
  – there is still an experienced higher difficulty though

Relation of reversible computation to quantum computation

Reversible computation is an absolutely necessary prerequisite for quantum computation stretches between state collapsing measurements from the outside.
A destructive overwrite of a specific bit would amount to a collapse of the state and a collapse
of the local "micro-multiverse" that constitutes the quantum computation.

After the code for the quantum computation is set up and is set in motion it's hand's off.
Of course parts of the running code can (and must be able to) influence other parts of the running code.
But such hidden internal internal interactions just splits up the quantum parallel entanglement of states even further.
All possibilities are kept till the final measurement from our single one common reality (our quantum mechanical frame of reference)
That measurement from outside (which may collapse the computation partially or completely) breaks the streak of reversibility.

Energy swinging frequency

In reversible computing devices energy needs to swing back and forth. If energy is moved back to the main energy storage source possibly every cycle (possibly through lots of mechanical differentials) friction losses will become too high.

For every stiff material there is a natural resonance frequency characteristic for size. If the swinging of energy is kept maximally local thus minimal in size the natural resonance frequency will be very high enforcing a too high operation speed with too much friction again.

Some optimal point in-between these two extremes must be found. To lower the resonance frequency the springs must be made more compliant and/or the mass must be made bigger.

(TODO: add the scaling law math for the resonance frequency of rotative and reciprocative resonators - how to scale the springs?)

Related

• Well merging

• Nanomechanical computation
• Quantum computation, Non mechanical technology path#quantum computation
• purely functional programming

• Nanomechanical computation and mechanical computation
• Rod logic, Buckling logic, Rotating link logic

• Energy recuperation
• Sharing of energy devaluations for a defined arrow of time in the mechanosynthesis in nanofactories:
  Dissipation sharing
• Reversible actuation
• Low speed efficiency limit
• Formal systems

• Compute architectures

External links

• Very informative slides (PPT):
  Reversible Computing Theory I: Reversible Logic Models flash version
  Principles of Adiabatic Processes These slides includes well merging for reversible adiabatic registers.
  (use the download option if you don't have flash installed/working)

• Reversible arithmetic logic unit for quantum arithmetic 2010 by Michael Kirkedal Thomsen, Robert Glück and Holger Bock Axelsen
  further Papers by Robert Glück et.al.
• RevComp - Actual implementations of reversible (electronic) circuits on chips

• Report 46 of the Institute fro Molecular Manufacturing: Molecular Mechanical Computing Sytems (2016-04) (pdf)

• Wikipedia: functional programming
• Wikipedia: reversible computing

• Wikimedia commons (de): causal depencency cone (wiki-TODO: integrate that image (or a similar translated one) here)

TODO Notes

• note reversible cascades – DONE
• analogy with harmonic oscillator - assymetric - energy backflow
• splitup into many paths via distributing gears (differential / planetary) (analogy electric nodes and transformers)
• link logistic data transmission rods
• pros & cons of rotative logic - reconfigurativability - space use

• why functional programming matters for AP technology – See: Purely functional programming
• reversible 1:1 IO mapping - pure functions
• low and high level programming languages
• relevance for multicore parallel computation

• classical reversible gates