Difference between revisions of "File:0415tenseBear.gif"
(added original text) |
|||
| Line 14: | Line 14: | ||
Operation in the stable attractive-force regime reduces bearing stiffness (which falls to zero at the threshold of instability), but also reduces the interatomic couplings that produce dynamic drag. | Operation in the stable attractive-force regime reduces bearing stiffness (which falls to zero at the threshold of instability), but also reduces the interatomic couplings that produce dynamic drag. | ||
| + | |||
| + | ---- | ||
| + | '''How can large interatomic repulsions increase static friction and energy dissipation?''' <br> | ||
| + | 🔘 [https://web.archive.org/web/20160314100841/http://e-drexler.com/p/04/02/0315pairSnap.html Softly supported sliding atoms can undergo abrupt transitions in energy (via internet archive)] | ||
| + | ---- | ||
| + | '''Bearing stiffness, dynamic energy dissipation:''' <br> | ||
| + | Drexler, K. E. (1992) Nanosystems: Molecular Machinery, Manufacturing, and Computation. Wiley/Interscience, pp.289-293. | ||
| + | |||
| + | = Related here on this wiki = | ||
| + | |||
| + | * [[Negative pressure bearings]] | ||
| + | * [[Levitation]] | ||
| + | * [[Snapback]] | ||
Latest revision as of 16:45, 5 November 2023
Source: https://web.archive.org/web/20160314130257/http://e-drexler.com/p/04/03/0322nonrepulsive.html
Author: Eric K. Drexler
"attractive interfaces"
Associated text from Eric's Website
Bearings can be stable despite attractive interactions between their surfaces
Intuitively, it might seem that a shaft-in-sleeve bearing can be stable only if the surfaces repel one another, pushing the shaft to the center of the sleeve. A closer examination shows that this condition is not necessary.
Consider a shaft centered in a sleeve (here illustrated in schematic cross-section A). By symmetry, the forces on the shaft cancel, but stability requires something more — that the potential energy as a function of displacement have a positive curvature, creating positive mechanical stiffness. This will obviously be the case when the surfaces are at their equilibrium separation (at a minimum of the intersurface potential) or closer (as shown in A).
The situation at greater separations becomes clear when one considers that the potential for displacement of the shaft equals the sum of the potentials for the opposed surfaces, as illustrated in the diagrams on the right. Where this combined potential retains a positive curvature (as shown in B), the centered position remains stable, even though the net intersurface force is attractive. (At still greater separations, as shown in C, the potential well bifurcates and the centered postion becomes unstable.)
Operation in the stable attractive-force regime reduces bearing stiffness (which falls to zero at the threshold of instability), but also reduces the interatomic couplings that produce dynamic drag.
How can large interatomic repulsions increase static friction and energy dissipation?
🔘 Softly supported sliding atoms can undergo abrupt transitions in energy (via internet archive)
Bearing stiffness, dynamic energy dissipation:
Drexler, K. E. (1992) Nanosystems: Molecular Machinery, Manufacturing, and Computation. Wiley/Interscience, pp.289-293.
Related here on this wiki
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 23:35, 17 September 2021 | 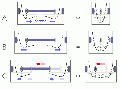 | 416 × 309 (11 KB) | Apm (Talk | contribs) | Source: https://web.archive.org/web/20160314130257/http://e-drexler.com/p/04/03/0322nonrepulsive.html <br> Author: Eric K. Drexler |
- You cannot overwrite this file.
File usage
The following 3 pages link to this file: