Difference between revisions of "Levitation"

From apm
Jump to: navigation, search
m (→‎Casimir force)
m (→‎Magnetic levitation: added linebreak)
 
(41 intermediate revisions by the same user not shown)
Line 1: Line 1:
  
 
With Levitation one can '''bear very high speeds in a very small space when load isn't excessive'''.
 
With Levitation one can '''bear very high speeds in a very small space when load isn't excessive'''.
 +
It offers friction levels even lower than [[superlubrication]].
 +
If even less friction is needed sufficient emty space surrounding the movement trajectory is needed to do throw and catch maneuvers through vacuum.
  
−
= Methods =
+
= Strong constraint levitation =
  
−
== Dynamic electrostatic control ==
+
== Negative compression bearings ==
  
−
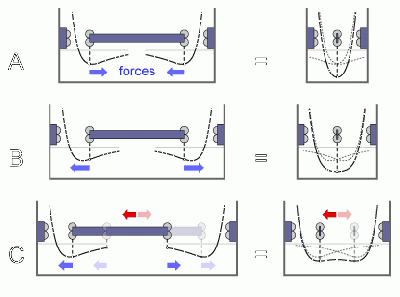
Some form of [[sensors|electrostatic sensor]] is needed. <br>
+
[[File:0415tenseBear.gif|400px|thumb|right|Bearings can be stable despite attractive interactions between their surfaces – Graphic by Eric K. Drexler]]
−
A lot should be nown from MEMS here.
+
  
−
== Electrostatic lagrange points ==
+
When bushing and axle of a [[diamondoid molecular element|DMME]]-bearing form an increasingly big but not too big gap the force can switch from inward from all directions to pulling outward in all directions at the same time but still
 +
provide a stable center for the axle. This lowers the waviness and coupling of the bearing and makes it more levitation like.
  
−
Mechanically forcing two equal e.g. positive charges with sufficient difference in charge [factor 24.65 = 25/2+sqrt(621)/2]
+
This happens whe the shafts surface lies between the minimum and the inflection point of the [//en.wikipedia.org/wiki/Lennard-Jones_potential Lennard Jones potential] of the bushing atoms. Going beyond the inflection point (unloaded bearing) makes the axle stick to one side of the bushing. Going for the minimum of the potential leds to zero local stiffness (like in [[tensegrity]] structures).
−
to circle around each other around their hypothetical barycenter with their hypothetical natural rotation period
+
−
gives two stable [//en.wikipedia.org/wiki/Lagrangian_point Lagrange points] in L3 L4 for small charges of the opposite sign - just like in celestial mechanics.
+
−
The ability to deviate from the natural movement might allow for further optimisation of the stable points.
+
−
['''To inverstigate:''' is there a better and if is there an optimal configutation]
+
−
The usefulnes of this isn't quite obvious.
+
  
−
Note that any (sufficiently isolated) zero dimensional nano sized object is subject to quantum mechanical wave dispersion.
+
Main article: [[Negative pressure bearings]]
 +
 
 +
== Active electrostatic levitation - (dynamic control) ==
 +
 
 +
In order to levitate a bearing make its parts repulse each other by:
 +
* Giving the shaft the opposite charge of the sleeve
 +
* Giving the axle the opposite charge of the wheel
 +
<small>The latter is same exact idea just swapped out what rotates and what not.</small>
 +
 
 +
=== No static levitation like such possible? ===
 +
 
 +
Static levitation this is likely impossible to be stable analogously <br>
 +
to Earnshaw theorem in the magnetostatic case. {{wikitodo|Check that}} <br>
 +
=> So some form of active control of the charges is needed <br>
 +
which in turn requires closed loop control and <br>
 +
some form of [[sensors|electrostatic sensing]]. <br>
 +
 
 +
The idea is to actively adjust the charge on the bearing components such that they  <br>
 +
remains in a nominal range for acceptable positions.
 +
 
 +
"Dynamic electrostatics" sounds kind of like an oxymoron. <br>
 +
Better say: "Actively controlled electrostatic levitation". <br>
 +
The point is: The dynamic part from active control is still slow enough to <br>
 +
not cause significant issues with radiation of electromagnetic waves. Thus electro'''statics'''. <br>
 +
Two different timescales here.
 +
 
 +
=== Existing work/research? ===
 +
 
 +
There might be knowledge from existing work with MEMS here. <br>
 +
'''Note that a lot of content about many electrostatic levitation on the web is of very different nature.''' <br>
 +
Macroscopic electrostatic levitation with such high electric fields that there are corona discharges. <br>
 +
This is not at all what we want here since it means electric energy losses and high energy electrons. <br>
 +
Actually we want to keep the gaps between the moving parts big enough and <br>
 +
voltages low enough for there to be not even excessive undesired electronic tunneling or even electron emission.
 +
 
 +
As of 2022 it seems that there's actually surprisingly little work out there about <br>
 +
high efficiency electrostatic levitation of small (microscale or smaller) machinery. <br>
 +
{{wikitodo|dig deeper about high efficiency microscale contact-less electrostatic levitation}}
 +
 
 +
=== Issues / challenges ===
 +
 
 +
'''Issue #1:'''<br>
 +
A homogeneously charged hollow sphere actually has no electric fields inside that originate from the charges on the surface <br>
 +
(a result of spherical symmetry and Gauss' law that links enclosed charge in a volume with electric fieldy penetrating out of that volume),<br>
 +
so a smaller sphere inside with the same charge will actually not be repulsed to the center.
 +
 
 +
So other geometric configurations deviant from perfect spherical symmetry need to be taken. <br>
 +
Also there's the question of the charges being mobile or fixed. <br>
 +
Mobile charges lead to counter-charge induction which may further destabilize rather than stabilize the situation.
 +
 
 +
'''Issue #2:'''<br>
 +
How to get the charge to the moving element that does not have any physical connection via covalent bonds to the machinery frame?
 +
Some ideas:
 +
* Charging the levitated part up by a sharp tip high field discharge? High energy electrons might damage bonds.
 +
* Charging up in physical and electrical contact pre-operation and then releasing that contact?
 +
* Use fixed permanent electric dipoles on the rotor that are enforced by electornegativity of used elements? <br>This is maybe too weak and short range? [https://en.wikipedia.org/wiki/Electret (Wikipedia: Elecret)]
 +
 
 +
=== Size of actively controlled electrostatic bearings ===
 +
 
 +
Given active sensing and closed loop control is needed <br>
 +
these likely wont be the very smallest bearings.
 +
 
 +
Also the bigger the gap the smoother the fields and the lower the losses. <br>
 +
Electrostatic levitation might be one of the if not the nanoscale bearing technologies with the lowest possible friction.
  
 
== Casimir force ==  
 
== Casimir force ==  
  
−
Beside thermally induced dipoles there's also a not yet well understood but certainly practical relevant component of the Van der Waals force
+
Eric Drexlers Blog (2009/04/20) about the Casimir force: [https://web.archive.org/web/20160304045629/http://metamodern.com/2009/04/20/casimir-effect-and-nanomachines/]<br>
−
that originate from the suppression of non harmonic modes of heat radiation in nano to micro scaled gaps.
+
Citation: "Lifshitz subsumes Casimir, and both correct London ''downwards''"
−
Certain geometries like an elongated ellipsoid over a circular hole in a plate) lead to static levitation.
+
−
['''Todo:''' find out why this shape]
+
  
−
== Negative compression bearings ==
+
From [[Nanosystems]] page 64 footnote: <br>
 +
The Casimir force is just a relativistic correction (taking retardation into account). <br>
 +
Making London dispersion forces fall off with r<sup>-7</sup> rather than r<sup>-6</sup> at larger separations. <br>
 +
In solution retardation effects become relevant as separations bigger than ~5nm (Israelachvili,1992).
  
−
When bushing and axle of a [[diamondoid molecular element|DMME]]-bearing form an increasingly big but not too big gap the force can switch from inward from all directions to pulling outwasd in all directions at the same time but still
+
{{wikitodo|understand how this relates to the picture of the suppression of virtual photons between metallic plates and explain this comprehensibly}}
−
provide a stable center for the axle. This lowers the waviness and coupling of the bearing and makes it more levitation like.
+
  
−
This happens whe the shafts surface lies between the minimum and the inflection point of the [//en.wikipedia.org/wiki/Lennard-Jones_potential Lennard Jones potential] of the bushing atoms. Going beyond the inflection point (unloaded bearing) makes the axle stick to one side of the bushing. Going for the minimum of the potential leds to zero local stiffness (like in tensegrity structures).
+
{{Todo|find the paper (stuff below) - what was up with this??}} <br>
 +
<small> Certain geometries like an elongated ellipsoid over a circular hole in a plate) lead to static levitation. </small>
  
 
== Magnetic levitation ==
 
== Magnetic levitation ==
  
−
Magnetism dooes not scale well with shrinking size thus it will only be used for levitating macroscopic parts.
+
Magnetism does not scale well with shrinking size it becomes very weak at the nanoscale thus it's <br>
 +
mainly useful in levitating macroscopic parts. <br>
 
The manipulation of magnetic properties of diamondoid materials falls unther the [[non mechanical technology path]]
 
The manipulation of magnetic properties of diamondoid materials falls unther the [[non mechanical technology path]]
 +
 +
=== Impossibility of purely magnetostatic levitation ===
 +
 +
Magnetostatic levitation is fundamentally impossible. <br>
 +
This is a result of [https://en.wikipedia.org/wiki/Earnshaw%27s_theorem Earnshaw's theorem] <br>
 +
This does not apply to magnetodynamic levitation or some other nonmagnetic effects. <br>
 +
In contrast to the macroscale there are more effects that can be exploited at the micro and nanoscale.
 +
 +
Given a one point support magnetostatic levitation for the remaining degrees of freedom is possible (to check).
 +
 +
= Weak constrain levitation =
 +
 +
== Passive electrostatic levitation ==
 +
 +
[[File:1600px-Orbitrap mass analyzer - partial cross-section.JPG|300px|thumb|right|Electrostatic operating particle traps (like this orbitrap at this macroscopic or much smaller microscopic scale) could be used to levitate even small [[crystolecule]]s. Charge per mass ration is much lower than for ions. Such levitated crystolecules will likely quantum disperse in orientation and position. But they may "bake together" a bit in their quantum frame of reference in case Van der Waals force exceeds mutual electrostatic repulsion. Note that this is just guessing for now.]]
 +
 +
The following means of levitation provide only weaker positional constraint. <br>
 +
Especially orientation of molecules it typically not preserved (to investigative). <br>
 +
This is no longer in [[machine phase]]. Well there may be a context dependent [[machine phase transition]]. <br>
 +
Levitated objects are still trapped (otherwise they would not be levitated but only guided of completely uncontrolled and free) <br>
 +
Thus weakly constrained levitated objects are "[[trapped free particles]]".<br>
 +
Related: [[Quantum dispersed crystolecules]]
 +
 +
The following two require charged particles:
 +
* [https://en.wikipedia.org/wiki/Orbitrap Orbitrap]
 +
* [https://en.wikipedia.org/wiki/Quadrupole_ion_trap Quadrupole ion trap (aka Paul trap)] – dynamic active leviation
 +
* generally: [https://en.wikipedia.org/wiki/Ion_trap Ion trap]
 +
 +
Optical:
 +
* [https://en.wikipedia.org/wiki/Optical_tweezers Optical trap (aka optical tweezers)] – dynamic active leviation
 +
 +
== Electrostatic Lagrange points ==
 +
 +
{{speculativity warning}}
 +
 +
By using mechanical constraints (bearings without levitation) to force two point charges
 +
* of same sign and
 +
* with sufficient difference in charge ( factor 24.65 = 25/2 + sqrt(621)/2 )
 +
to circle around each other
 +
* around their hypothetical barycenter
 +
* with their hypothetical natural rotation period
 +
should give two stable [//en.wikipedia.org/wiki/Lagrangian_point Lagrange points] in L3 L4 for small charges of the opposite sign.
 +
Just like in celestial mechanics.
 +
 +
The ability to deviate from the natural movement might allow for further optimization of the stable points. <br>
 +
{{todo|Investigate whether there a better configuration and if is there an optimal configuration}} <br>
 +
 +
The two charges that generate the electrostatic Lagrange points need to move. <br>
 +
And the bearings that are necessary for that motion are not assumed to be levitated. <br>
 +
So this strategy is not a means to reduce friction.
 +
 +
Note that this unlike many electrostatic traps is 3D point charges rotating in a 2D plane.
 +
 +
Note that any (sufficiently isolated) zero dimensional nano sized object is subject to notable quantum mechanical wave dispersion and tunneling (meaning in colorful words that it kind of "dissolves" an reappears somewhere else by chance).
 +
 +
'''Applications:''' The eventual usefulness of this isn't quite obvious. <br>
 +
 +
= Misc =
 +
 +
There is also the method of optical tweezers (and smaller plasmonic tweezers) which could be counted as "levitation methods".
 +
(Note that these methods are likely insufficient in stiffness and force for single atom placement especially in advanced mechanosysnthesis.)
 +
 +
Also there is sonic "levitation" for bigger things immersed in gases. The contact to a gas comes with much higher friction though.
  
 
= Applications =
 
= Applications =
  
−
* nanoscale turbomelecular pumps (but the may not be needed since positive displacement pumps do just fine)
+
Since [[Friction in gem-gum technology|dynamic drag in crystolecule bearings]] can be significant for higher speeds: <br>
 +
Levitation can provide a further mean for reducing friction where high speed motion is needed. <br>
 +
Especially of the smallest scales. <br>
 +
Otherwise due to high heating from friction operation at high speeds is limited to
 +
* short bursts in time exclusive or
 +
* small spots in space
 +
 
 +
== More concrete application examples ==
 +
 
 +
* generating RF radiation by rotating very many charged nanoscale rotors very fast - as a phased array
 +
* nanoscale turbo-molecular pumps (but the may not be needed since [[positive displacement pumps]] do just fine)
 
* [[carriage particle accelerators]]
 
* [[carriage particle accelerators]]
 
* [[Medium movers|moving surface medium movers]]
 
* [[Medium movers|moving surface medium movers]]
 +
 +
= Related =
 +
 +
* [[Superlubrication]]
 +
* [[Infinitesimal bearing]]
 +
* [[Negative pressure bearings]]
 +
 +
= External links =
 +
 +
* [http://e-drexler.com/p/04/03/0322nonrepulsive.html Bearings can be stable despite attractive interactions between their surfaces] (at K. Eric Drexlers website)
 +
* [[Wikipedia:Q factor]]
 +
----
 +
* Closed-loop control active levitation – Wikipedia: [https://en.wikipedia.org/wiki/Open-loop_controller Open-loop_controller Open-loop controller]
 +
----
 +
* Wikipedia: [https://en.wikipedia.org/wiki/Earnshaw%27s_theorem Earnshaw's theorem] (proof of fundamental impossibility of purely magnetostatic levitation)

Latest revision as of 17:51, 12 March 2022

With Levitation one can bear very high speeds in a very small space when load isn't excessive. It offers friction levels even lower than superlubrication. If even less friction is needed sufficient emty space surrounding the movement trajectory is needed to do throw and catch maneuvers through vacuum.

Strong constraint levitation

Negative compression bearings

Bearings can be stable despite attractive interactions between their surfaces – Graphic by Eric K. Drexler

When bushing and axle of a DMME-bearing form an increasingly big but not too big gap the force can switch from inward from all directions to pulling outward in all directions at the same time but still provide a stable center for the axle. This lowers the waviness and coupling of the bearing and makes it more levitation like.

This happens whe the shafts surface lies between the minimum and the inflection point of the Lennard Jones potential of the bushing atoms. Going beyond the inflection point (unloaded bearing) makes the axle stick to one side of the bushing. Going for the minimum of the potential leds to zero local stiffness (like in tensegrity structures).

Main article: Negative pressure bearings

Active electrostatic levitation - (dynamic control)

In order to levitate a bearing make its parts repulse each other by:

  • Giving the shaft the opposite charge of the sleeve
  • Giving the axle the opposite charge of the wheel

The latter is same exact idea just swapped out what rotates and what not.

No static levitation like such possible?

Static levitation this is likely impossible to be stable analogously
to Earnshaw theorem in the magnetostatic case. (wiki-TODO: Check that)
=> So some form of active control of the charges is needed
which in turn requires closed loop control and
some form of electrostatic sensing.

The idea is to actively adjust the charge on the bearing components such that they
remains in a nominal range for acceptable positions.

"Dynamic electrostatics" sounds kind of like an oxymoron.
Better say: "Actively controlled electrostatic levitation".
The point is: The dynamic part from active control is still slow enough to
not cause significant issues with radiation of electromagnetic waves. Thus electrostatics.
Two different timescales here.

Existing work/research?

There might be knowledge from existing work with MEMS here.
Note that a lot of content about many electrostatic levitation on the web is of very different nature.
Macroscopic electrostatic levitation with such high electric fields that there are corona discharges.
This is not at all what we want here since it means electric energy losses and high energy electrons.
Actually we want to keep the gaps between the moving parts big enough and
voltages low enough for there to be not even excessive undesired electronic tunneling or even electron emission.

As of 2022 it seems that there's actually surprisingly little work out there about
high efficiency electrostatic levitation of small (microscale or smaller) machinery.
(wiki-TODO: dig deeper about high efficiency microscale contact-less electrostatic levitation)

Issues / challenges

Issue #1:
A homogeneously charged hollow sphere actually has no electric fields inside that originate from the charges on the surface
(a result of spherical symmetry and Gauss' law that links enclosed charge in a volume with electric fieldy penetrating out of that volume),
so a smaller sphere inside with the same charge will actually not be repulsed to the center.

So other geometric configurations deviant from perfect spherical symmetry need to be taken.
Also there's the question of the charges being mobile or fixed.
Mobile charges lead to counter-charge induction which may further destabilize rather than stabilize the situation.

Issue #2:
How to get the charge to the moving element that does not have any physical connection via covalent bonds to the machinery frame? Some ideas:

  • Charging the levitated part up by a sharp tip high field discharge? High energy electrons might damage bonds.
  • Charging up in physical and electrical contact pre-operation and then releasing that contact?
  • Use fixed permanent electric dipoles on the rotor that are enforced by electornegativity of used elements?
    This is maybe too weak and short range? (Wikipedia: Elecret)

Size of actively controlled electrostatic bearings

Given active sensing and closed loop control is needed
these likely wont be the very smallest bearings.

Also the bigger the gap the smoother the fields and the lower the losses.
Electrostatic levitation might be one of the if not the nanoscale bearing technologies with the lowest possible friction.

Casimir force

Eric Drexlers Blog (2009/04/20) about the Casimir force: [1]
Citation: "Lifshitz subsumes Casimir, and both correct London downwards"

From Nanosystems page 64 footnote:
The Casimir force is just a relativistic correction (taking retardation into account).
Making London dispersion forces fall off with r-7 rather than r-6 at larger separations.
In solution retardation effects become relevant as separations bigger than ~5nm (Israelachvili,1992).

(wiki-TODO: understand how this relates to the picture of the suppression of virtual photons between metallic plates and explain this comprehensibly)

(TODO: find the paper (stuff below) - what was up with this??)
Certain geometries like an elongated ellipsoid over a circular hole in a plate) lead to static levitation.

Magnetic levitation

Magnetism does not scale well with shrinking size it becomes very weak at the nanoscale thus it's
mainly useful in levitating macroscopic parts.
The manipulation of magnetic properties of diamondoid materials falls unther the non mechanical technology path

Impossibility of purely magnetostatic levitation

Magnetostatic levitation is fundamentally impossible.
This is a result of Earnshaw's theorem
This does not apply to magnetodynamic levitation or some other nonmagnetic effects.
In contrast to the macroscale there are more effects that can be exploited at the micro and nanoscale.

Given a one point support magnetostatic levitation for the remaining degrees of freedom is possible (to check).

Weak constrain levitation

Passive electrostatic levitation

Electrostatic operating particle traps (like this orbitrap at this macroscopic or much smaller microscopic scale) could be used to levitate even small crystolecules. Charge per mass ration is much lower than for ions. Such levitated crystolecules will likely quantum disperse in orientation and position. But they may "bake together" a bit in their quantum frame of reference in case Van der Waals force exceeds mutual electrostatic repulsion. Note that this is just guessing for now.

The following means of levitation provide only weaker positional constraint.
Especially orientation of molecules it typically not preserved (to investigative).
This is no longer in machine phase. Well there may be a context dependent machine phase transition.
Levitated objects are still trapped (otherwise they would not be levitated but only guided of completely uncontrolled and free)
Thus weakly constrained levitated objects are "trapped free particles".
Related: Quantum dispersed crystolecules

The following two require charged particles:

Optical:

Electrostatic Lagrange points

Warning! you are moving into more speculative areas.

By using mechanical constraints (bearings without levitation) to force two point charges

  • of same sign and
  • with sufficient difference in charge ( factor 24.65 = 25/2 + sqrt(621)/2 )

to circle around each other

  • around their hypothetical barycenter
  • with their hypothetical natural rotation period

should give two stable Lagrange points in L3 L4 for small charges of the opposite sign. Just like in celestial mechanics.

The ability to deviate from the natural movement might allow for further optimization of the stable points.
(TODO: Investigate whether there a better configuration and if is there an optimal configuration)

The two charges that generate the electrostatic Lagrange points need to move.
And the bearings that are necessary for that motion are not assumed to be levitated.
So this strategy is not a means to reduce friction.

Note that this unlike many electrostatic traps is 3D point charges rotating in a 2D plane.

Note that any (sufficiently isolated) zero dimensional nano sized object is subject to notable quantum mechanical wave dispersion and tunneling (meaning in colorful words that it kind of "dissolves" an reappears somewhere else by chance).

Applications: The eventual usefulness of this isn't quite obvious.

Misc

There is also the method of optical tweezers (and smaller plasmonic tweezers) which could be counted as "levitation methods". (Note that these methods are likely insufficient in stiffness and force for single atom placement especially in advanced mechanosysnthesis.)

Also there is sonic "levitation" for bigger things immersed in gases. The contact to a gas comes with much higher friction though.

Applications

Since dynamic drag in crystolecule bearings can be significant for higher speeds:
Levitation can provide a further mean for reducing friction where high speed motion is needed.
Especially of the smallest scales.
Otherwise due to high heating from friction operation at high speeds is limited to

  • short bursts in time exclusive or
  • small spots in space

More concrete application examples

Related

External links

  • Wikipedia: Earnshaw's theorem (proof of fundamental impossibility of purely magnetostatic levitation)
Retrieved from "http://apm.bplaced.net/w/index.php?title=Levitation&oldid=12417"