Distorted visualization methods for convergent assembly

From apm
Jump to: navigation, search
Here mapped is both a c coordinate grid and molecular mill rotors analog to the ones seen in: "Productive Nanosystems from Molecules to Superproducts". Note that in non-transformed coordinates the grey wall sits on xy-plane partly above partly below. Thus it gets curls both ways in the magnifying log polar coordinates. The wide bottom is a small cutout around (0,0,0) that's necessary as nearing zero everything gets exponentially magnified.
Generalized log polar mapping across two assembly layers. This should be extendable to more. Big caveat here is that assembly layers need to be roughly same sub-layer number which is not at all the case for the lowermost assembly layers. Hard coded assembly lines makes for very many sub-layers.

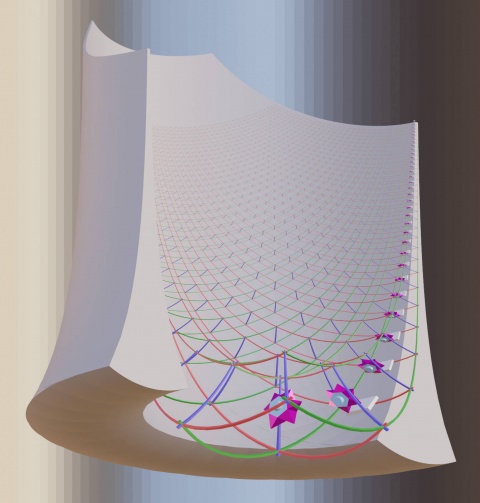
To get a complete picture of the physical layout of all the assembly levels of the convergent assembly in a nanofactory (which might be organized in a stack of coplanar layers) and see all of this in one single image at one glance one needs to project space in a nonlinear way.
Normal perspective (a linear projection) is unsuitable since it compresses most details towards the horizon. Instead a nonlinear polar logarithmic mapping is the best fit.

An additional difficulty is that a nanofactory as opposed to a map is inherently three dimensional so some cross cut has to be chosen. Whether that cross cut can be simply planar or not depends on the exact design choices taken in a concrete nanofactories design.

(wiki-TODO: add image [1] -- license?)

Displaying many scales and their relation simultaneously

This can be done by generalizing log polar mapping to 3D like so:

  • x'(x,y,z) = pi/2 - atan2( z, sqrt(pow(x,2) + pow(y,2)) ) * cos(atan2(y,x)))
  • y'(x,y,z) = pi/2 - atan2( z, sqrt(pow(x,2) + pow(y,2)) ) * sin(atan2(y,x)))
  • z'(x,y,z) = log( sqrt(pow(x,2) + pow(y,2) + pow(z,2)) ) / log(base)

Related

Distorted visualization methods (like e.g. the 3D log polar mapping visualization method) may also be useful to keep oriented in the visualizations of
abstract spaces other than concrete physical space. E.g. circuitry topology in very large software systems.

Hyperbolic geometry and Escher disks

Related to this: https://en.wikipedia.org/wiki/Circle_Limit_III

Problem #1:
Not all scales are treated the same. More precisely:
The mapping does not transform scale invariance into translational symmetry (as log polar does).
Infinitely big things get crunched into finite space. A singularity at the perimeter. Even when exponentially/geometrically growing.
(Not sure if you can explode the rim when growing uber expeonentially with an essential singularity, doubt so even then, fascinating math problem but beside the practical focus here.)

Problem #1: The depiction is inherently 2D.

Vertical cut:
Projecting to an Escher disk a vertical cut through exponentially growing assembly levels with bottom at the disks center this would give only the top half of a disk. Above the center shrinking down the growing size layers but soon too much. Sideways already small things get shrunk down too pointlessly.
So overall not a particularly good choice for a coordinate transformation.

Horizontal single plane cut through already log polar transformed coordinates:
This gives a disk looking similar to an Escher disk but it would be very different in nature.
Transforming a planar disk from log polar back to original coordinates gives an spherical (half)shell.
With exponentially shrinking assembly levels nearing the xy-plane there is much stuff compressed to near the edges of the disks.
Well limited by the smallest assembly level of course as we have physics not pure math.
This is really not suitable for showing thinsg at multiple scales simultaneously.
Also note that the observation angle within a deisk changes like on a sphere as well in the original coordinates we are on a sphere
(nonequidistantly sampled sphere to highlight peculiarity).

External Links

  • An interactive online map spanning a wide range of scales: mercator extreme
    The mercator projection cut off much closer to the poles whichs location can be freely chosen.
  • python scripts to generate log-polar maps from pixelgraphics [2]
  • "Detail-In-Context Visualization for Satellite Imagery" [3]
    "Complex Logarithmic Views for Small Details in Large Contexts" [4]
    by Joachim Boettinger et. al.
    Department of Computer and Information Science, University of Konstanz, Germany
  • Video showing a manual multi-scale zoom device [5] the "zoom-scope"
  • square grid mapped to show details on all scales equally [6]
  • More large scale map examples [7]

Keywords

distortion lens view; log-polar map; complex logarithmic map, complex logarithmic view, anamorphic mirror, anamorphosis

Related

Retrieved from "http://apm.bplaced.net/w/index.php?title=Distorted_visualization_methods_for_convergent_assembly&oldid=15928"