Levitation
With Levitation one can bear very high speeds in a very small space when load isn't excessive. It offers friction levels even lower than superlubrication. If even less friction is needed sufficient emty space surrounding the movement trajectory is needed to do throw and catch maneuvers through vacuum.
Contents
Strong constraint levitation
Negative compression bearings
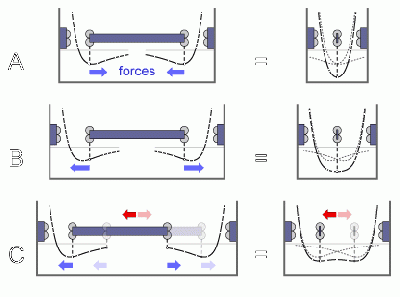
When bushing and axle of a DMME-bearing form an increasingly big but not too big gap the force can switch from inward from all directions to pulling outward in all directions at the same time but still provide a stable center for the axle. This lowers the waviness and coupling of the bearing and makes it more levitation like.
This happens whe the shafts surface lies between the minimum and the inflection point of the Lennard Jones potential of the bushing atoms. Going beyond the inflection point (unloaded bearing) makes the axle stick to one side of the bushing. Going for the minimum of the potential leds to zero local stiffness (like in tensegrity structures).
Main article: Negative pressure bearings
Dynamic electrostatic control
Charge on the bearing sleeve is dynamically adjusted such that the rotor remains in a nominal position. The free floating rotor rotor needs to be charged
- either by featuring electrostatic dipoles
- or by shooting over electrons maybe
- or ...
Some form of electrostatic sensor is needed.
A lot should be known from existing work with MEMS here.
Casimir force
Eric Drexlers Blog (2009/04/20) about the Casimir force: [1]
Citation: "Lifshitz subsumes Casimir, and both correct London downwards"
From Nanosystems page 64 footnote:
The Casimir force is just a relativistic correction (taking retardation into account).
Making London dispersion forces fall off with r-7 rather than r-6 at larger separations.
In solution retardation effects become relevant as separations bigger than ~5nm (Israelachvili,1992).
(wiki-TODO: understand how this relates to the picture of the suppression of virtual photons between metallic plates and explain this comprehensibly)
(TODO: find the paper (stuff below) - what was up with this??)
Certain geometries like an elongated ellipsoid over a circular hole in a plate) lead to static levitation.
Magnetic levitation
Magnetism does not scale well with shrinking size it becomes very weak at the nanoscale thus it's mainly useful in levitating macroscopic parts. The manipulation of magnetic properties of diamondoid materials falls unther the non mechanical technology path
Impossibility of purely magnetostatic levitation
Magnetostatic levitation is fundamentally impossible.
This is a result of Earnshaw's theorem
This does not apply to magnetodynamic levitation or some other nonmagnetic effects.
In contrast to the macroscale there are more effects that can be exploited at the micro and nanoscale.
Given a one point support magnetostatic levitation for the remaining degrees of freedom is possible (to check).
Weak constrain levitation

The following means of levitation provide only weaker positional constraint.
Especially orientation of molecules it typically not preserved (to investigative).
This is no longer in machine phase. Well there may be a context dependent machine phase transition.
Levitated objects are still trapped (otherwise they would not be levitated but only guided of completely uncontrolled and free)
Thus weakly constrained levitated objects are "trapped free particles".
Related: Quantum dispersed crystolecules
The following two require charged particles:
- Orbitrap
- Quadrupole ion trap (aka Paul trap) – dynamic active leviation
- generally: Ion trap
Optical:
- Optical trap (aka optical tweezers) – dynamic active leviation
Electrostatic Lagrange points
Warning! you are moving into more speculative areas.
By using mechanical constraints (bearings without levitation) to force two point charges
- of same sign and
- with sufficient difference in charge ( factor 24.65 = 25/2 + sqrt(621)/2 )
to circle around each other
- around their hypothetical barycenter
- with their hypothetical natural rotation period
should give two stable Lagrange points in L3 L4 for small charges of the opposite sign. Just like in celestial mechanics.
The ability to deviate from the natural movement might allow for further optimization of the stable points.
(TODO: Investigate whether there a better configuration and if is there an optimal configuration)
The two charges that generate the electrostatic Lagrange points need to move.
And the bearings that are necessary for that motion are not assumed to be levitated.
So this strategy is not a means to reduce friction.
Note that this unlike many electrostatic traps is 3D point charges rotating in a 2D plane.
Note that any (sufficiently isolated) zero dimensional nano sized object is subject to notable quantum mechanical wave dispersion and tunneling (meaning in colorful words that it kind of "dissolves" an reappears somewhere else by chance).
Applications: The eventual usefulness of this isn't quite obvious.
Misc
There is also the method of optical tweezers (and smaller plasmonic tweezers) which could be counted as "levitation methods". (Note that these methods are likely insufficient in stiffness and force for single atom placement especially in advanced mechanosysnthesis.)
Also there is sonic "levitation" for bigger things immersed in gases. The contact to a gas comes with much higher friction though.
Applications
- generating RF radiation by rotating very many charged nanoscale rotors very fast - as a phased array
- nanoscale turbo-molecular pumps (but the may not be needed since positive displacement pumps do just fine)
- carriage particle accelerators
- moving surface medium movers
Related
External links
- Bearings can be stable despite attractive interactions between their surfaces (at K. Eric Drexlers website)
- Wikipedia:Q factor
- Closed-loop control active levitation – Wikipedia: Open-loop_controller Open-loop controller
- Wikipedia: Earnshaw's theorem (proof of fundamental impossibility of purely magnetostatic levitation)